Covarianza, valores propios, varianza y todo.
Shubham Panchal septiembre de 2022 Hacia la ciencia de Datos https://towardsdatascience.com/
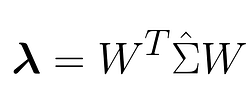
El análisis de componentes principales (PCA) es una técnica popular para reducir las dimensiones de los datos y se incluye en la mayoría de los cursos de ML/DS en la sección «aprendizaje no supervisado». Hay varios blogs que explican PCA junto con videos de YouTube, entonces, ¿por qué está este blog aquí?
¿Otro blog sobre PCA?
Como estudiante de ML que ama más las matemáticas, encontré todos los blogs sobre PCA incompletos. Al resumir cada blog que leí, solo pude llegar a una conclusión cada vez: » PCA maximiza la variación de los puntos de datos proyectados » y no me equivoqué en ninguna parte. Pero como descubrí solo esta perspectiva en todas partes, no pude profundizar en el tema para saber más sobre las matemáticas y cómo los valores propios de repente entraron en escena.
https://towardsdatascience.com/media/2ddb5bb30a41babc4869c8930f80c011
Historias del autor
Decidí tomar esto en serio y recopilé libros, foros y otros blogs para producir este blog que escribí. Contiene matemáticas no tan fáciles, pero te garantizo que ningún concepto te mantendrá rascándote la cabeza durante más de 10 minutos. Esta historia está destinada a lectores que,
- Curioso por conocer las matemáticas detrás de PCA
- Consciente de conceptos de álgebra lineal como base, traza de una matriz, valores propios y descomposición propia.
- Consciente de conceptos estadísticos como variables aleatorias, vectores aleatorios, varianza y covarianza.
¡Cuéntame cómo te va!
Pequeño descargo de responsabilidad
Las matemáticas involucradas aquí utilizarán términos complejos del álgebra lineal y la estadística. Cada nuevo término introducido en la historia se etiquetará con un recurso al que se puede consultar para obtener más conocimientos sobre ese término.
El problema
El objetivo principal del PCA es explicar las variables observadas dadas (los datos) en un conjunto de variables latentes de modo que las variables latentes retengan la mayor parte de la información de las variables observadas.
Las variables observadas son aquellas variables cuyo valor real se mide. Considerando un problema en el que se nos pide modelar el precio de una acción en particular, las variables observadas podrían ser las inversiones realizadas por la empresa, las ventas, los rendimientos y otras variables que pueden influir directamente en el precio de la acción.
La palabra «latente» significa oculto u oculto. En nuestro caso, las variables que no se observan directamente, sino que se infieren con la ayuda del modelo utilizado en las variables observadas. En el mismo ejemplo de predicción del precio de las acciones, las variables latentes podrían ser las posibilidades de que una persona compre esas acciones, el precio futuro de esas acciones, etc.
En el caso de PCA, el objetivo es,
Determine las variables latentes de modo que contengan la mayor parte de la información contenida en las variables observadas. El número de variables latentes debe ser menor que el número de variables observadas.
¿Por qué no podemos simplemente copiar algunas características de nuestro conjunto de datos para reducir las dimensiones?
En la mayoría de los conjuntos de datos del mundo real, las características o variables observadas dependen unas de otras hasta cierto punto. Por ejemplo, en un conjunto de datos meteorológicos, la cantidad de lluvia recibida puede depender o no de la temperatura de una región en particular. Si eliminamos la variable de temperatura directamente, podríamos perder parte de la información útil contenida en la función. Por lo tanto, necesitamos transformar las variables observadas de tal manera que podamos eliminar fácilmente las características menos destacadas del conjunto de datos, preservando al mismo tiempo la información.
1. Encontrar una representación alternativa para los puntos de datos.
Primero, consideramos un conjunto de datos que contiene N muestras donde cada muestra tiene D características. Podemos representar nuestro conjunto de datos en forma de matriz X , donde cada fila contiene una muestra y cada columna corresponde a los valores de una característica particular.
En partes posteriores de la historia, también consideraríamos X como un vector aleatorio,
Donde hemos considerado cada característica como una variable aleatoria. No necesitas preocuparte por esto, como mencionaré claramente cuando consideremos X como un vector aleatorio.
Además, una suposición importante que hacemos es que los puntos de datos están centrados con respecto a la media. Podemos hacer esto restando el vector medio de cada muestra, de modo que los puntos de datos resultantes estén centrados alrededor de la media.
Deseamos representar estos puntos de datos utilizando nuevos vectores base. Una base es un conjunto de vectores independientes que abarcan su espacio vectorial ambiental. En términos más simples, una combinación lineal de todos los vectores en la base (o vectores de base) produce cada vector presente en el espacio vectorial. La nueva base proporcionará una representación alternativa de las funciones mediante la cual podemos eliminar fácilmente las funciones que son menos importantes. Al elegir una nueva base, también necesitaremos nuevas coordenadas para representar los puntos de datos.
Estos vectores base serían especiales ya que podremos elegir cuántos vectores base necesitamos para obtener el número deseado de dimensiones. Pero debemos elegir estas bases con cuidado, para que puedan generar casi exactamente los mismos puntos de datos, sin ninguna pérdida considerable . Para construir esa base, necesitaremos,
- Una base ortonormal para representar los puntos de datos de una manera alternativa (como se discutió anteriormente). El número de vectores base es igual a las dimensiones del espacio vectorial, por lo que en nuestro caso necesitaríamos D vectores base. Nuestra nueva base abarcará el mismo espacio vectorial en el que se encuentran nuestros puntos de datos. Entonces tendremos D vectores en la nueva base.
- Coordenadas para representar cada punto de datos x_i de forma única con la nueva base ortonormal.
Podemos definir una nueva base ortonormal en el espacio D-dimensional,
Al reunir todos estos vectores ortonormales en una matriz donde cada columna contiene un vector, nos queda una matriz ortogonal (que tiene algunas propiedades útiles que exploraremos en secciones posteriores),
A continuación, necesitaremos algunas coordenadas o pesos que se puedan multiplicar con la nueva base para representar los puntos de datos. La combinación ponderada de las coordenadas y los vectores base no representará exactamente el punto de datos, pero deseamos obtener una buena aproximación.
Para todos los N puntos de datos, las coordenadas serán diferentes, por lo que es bueno cambiar la notación matriz-vectorial,
2. Encontrar los parámetros óptimos
Deseamos obtener una aproximación cercana de nuestros puntos de datos utilizando la nueva base y las coordenadas. Para medir la ‘ cercanía ‘ del punto de datos x y su aproximación Wz , calculamos el promedio de la norma L2 al cuadrado (norma euclidiana) de todos los x-Wz,
Cuanto menor sea el valor de la función L (el valor de la función L es un escalar), mejor aproximación lograremos. Entonces, ahora nuestro problema entra en la teoría de la optimización, en la que necesitamos determinar los valores de W y Z que den el valor más bajo para L. Podemos calcular la derivada de L wrt z_n y equipararla a cero.
En el siguiente paso, vamos a calcular las derivadas parciales de la función objetivo con respecto a los vectores. Si no se siente cómodo con el cálculo matricial, puede consultar estas notas que contienen algunos resultados útiles y sus derivaciones.
Como prometimos, en el último paso de (7) estamos usando una excelente propiedad de las matrices ortogonales. A continuación, igualamos la derivada parcial obtenida en (8) a cero para obtener el valor óptimo de z en términos de W y x .
Como puede observar, el valor mínimo del objetivo L se obtiene cuando z_i son iguales a los puntos de datos x_i multiplicados por la transpuesta de la matriz W. Como el primer término en la expresión de nuestra función objetivo, Σ x_n^T x_n, es una constante, podemos eliminarlo y continuar expandiendo el término Σ z_n^T z_n,
La relación entre z y W es evidente en (9), pero debemos usarla hábilmente para obtener los resultados deseados.
Tenemos algunas propiedades del operador de seguimiento en la evaluación anterior,
El uso del operador de seguimiento es necesario aquí, ya que nos ayudará a obtener un resultado importante mediante el cual se calcula el valor óptimo de W. Además, hemos utilizado un resultado importante de las estadísticas,
La matriz de covarianza empírica K_XX es una matriz que contiene la covarianza entre diferentes pares de variables aleatorias contenidas dentro de un vector aleatorio. Esta expresión puede parecer poco convincente a primera vista, pero puede verificarla considerando puntos de datos 2D que producirían una matriz de covarianza de 2 * 2.
La matriz de covarianza también es simétrica, como podemos deducir fácilmente de (14). Las matrices simétricas también poseen algunas propiedades hermosas como,
- Las matrices simétricas tienen valores propios reales, ¡así que no hay cosas complejas!
- Los vectores propios correspondientes son ortogonales entre sí. Pueden actuar como una base excelente para espacios vectoriales, llamada base propia (¡espero que hayas entendido la pista!
Para determinar el valor óptimo de W, podemos configurar una función lagrangiana con el objetivo de,
En (11), observe que maximizar la traza daría como resultado la minimización de L’ . En nuestro problema de optimización, solo teníamos una restricción para W y esa es su ortogonalidad. Para mantener las cosas bien definidas en el contexto de los multiplicadores de Lagrange, hemos definido un producto interno matricial en la expresión anterior (14),
Se conoce como producto interno de Frobenius y toma dos matrices y devuelve un escalar (una propiedad típica de todos los productos internos). La matriz λ será una matriz cuadrada que contiene los multiplicadores,
A continuación, calculamos la derivada parcial del objetivo P respecto de W y la igualamos a cero para obtener los valores de λ .
La expresión anterior nos brinda el resultado más hermoso que hemos obtenido hasta ahora y aquí esperaremos para adorar su belleza.
El teorema espectral del álgebra lineal dice que una matriz simétrica es diagonalizable. Simplemente significa que una matriz simétrica se puede transformar en una matriz diagonal (donde los elementos solo se ubican en la diagonal principal de una matriz) mediante el uso de otras matrices especiales. La diagonalizabilidad es una propiedad excelente, ya que reduce en gran medida el cálculo de otras propiedades útiles como determinantes, trazas, etc. Una matriz simétrica A es diagonalizable, como,
donde D es la matriz diagonal derivada de A. Los elementos de D son los valores propios reales de la matriz A. Las columnas de la matriz P contienen los vectores propios de la matriz A. Como la matriz A es simétrica, los vectores propios son ortogonales entre sí, por lo que la matriz P también es ortogonal.
Volviendo a la expresión (18),
La matriz de covarianza K_XX es simétrica, por lo que la matriz diagonal λ contiene los valores propios de la matriz de covarianza y W contiene los vectores propios normalizados. Entonces, finalmente tenemos la base ortonormal W y las coordenadas z como,
Nuestro objetivo era encontrar una nueva representación para los puntos de datos para que las funciones se puedan eliminar fácilmente. Además, analizamos por qué las funciones no se pueden eliminar fácilmente, ya que dependen unas de otras. Lo que acabamos de hacer en los pasos (2) y (3) fue intentar hacer que estas funciones sean independientes entre sí para que podamos seleccionarlas fácilmente sin preocuparnos por las dependencias que tienen entre sí. Esto no es sólo una idea, sino que lo hemos demostrado matemáticamente con los pasos (2) y (3).
Retrocedamos en el tiempo y nos daremos cuenta de que la covarianza entre dos variables aleatorias captura aproximadamente la dependencia entre las variables. Si las dos variables son independientes, la covarianza es cero.
En la expresión (21), expresamos la matriz de covarianza K_XX como una matriz diagonal. En la matriz de covarianza, todas las entradas no diagonales indican las covarianzas entre pares de variables o características aleatorias. Al transformar la matriz de covarianza en una matriz diagonal, hemos destruido toda la covarianza presente entre las características/variables aleatorias. Hemos intentado hacer que cada característica sea independiente para que podamos clasificarlas fácilmente utilizando criterios adecuados, sin preocuparnos mucho por las dependencias internas.
Al minimizar la función L , nos hemos dado cuenta de que la mejor aproximación del punto de datos x_i podría obtenerse transformando la base del punto de datos a la nueva base que es la base propia .
3. Reducir las dimensiones (arrancar las características)
Hasta ahora hemos encontrado una nueva base para representar los puntos de datos de tal manera que podamos separar fácilmente las características sin pensar en la dependencia de una característica de otra. Pero la pregunta es: ¿qué funciones deberíamos eliminar? Necesitamos algún criterio para mantener las mejores características K del conjunto de datos.
Para PCA, elegiremos las funciones que tengan una mayor variación. La lógica simple es que las características con una varianza baja son tan buenas como las constantes y pueden tener poco o ningún impacto en la variable de respuesta. Aquí hay una buena discusión sobre CrossValidated sobre el mismo tema. Esta es también la razón por la que es posible que haya notado que VarianceThresholden el sklearn.feature_selectionmódulo para seleccionar funciones tiene una variación mayor que el umbral dado. Como comentamos anteriormente, la matriz de covarianza de nuestros datos K_XX parece una matriz diagonal en la nueva base,
Para la expresión anterior, hemos tratado z (el punto de datos transformado) como un vector aleatorio,
Las diagonales de la matriz de covarianza contienen las varianzas individuales de las características. Entonces, los valores propios corresponden a las varianzas de los puntos de datos transformados y deseamos elegir los valores propios K superiores . Además, de la matriz W , elegiremos los vectores propios K correspondientes y los usaremos para transformar finalmente el conjunto de datos.
Entonces, elegiremos K vectores propios donde la dimensión de cada vector propio sea D y los empaquetaremos en una matriz W_K, la transpondremos y la multiplicaremos con cada uno de los puntos de datos x_i para obtener las representaciones de dimensiones inferiores z_i .
Cuando elegimos K < D (las dimensiones reales de los datos), obtendremos una aproximación del punto de datos y no su representación precisa en la nueva base, simplemente porque descartamos los vectores de base de W. Así es como hemos reducido las dimensiones de los datos, eliminando funciones de forma inteligente.
Se trataba de PCA y su papel en la reducción de dimensionalidad.
¡Suspiro! ¡Eso fue mucha matemática!
https://towardsdatascience.com/media/2ddb5bb30a41babc4869c8930f80c011Otros cuentos del autor
Espero que la historia proporcione una imagen completa de PCA y su conexión con la covarianza, sus vectores propios y la reducción de dimensionalidad. ¡Hasta entonces, sigue aprendiendo matemáticas y que tengas un buen día por delante (si llegaste hasta aquí)!