Najib Sharifi PhD en Química Molecular | Ingeniero en Aprendizaje Automático. Nov. 2024. MEDIUM
Imaginemos a un niño pequeño que está aprendiendo a caminar. Da un paso y puede tropezar, pero con cada intento ajusta sus movimientos en función del éxito o el fracaso del paso anterior. Con el tiempo, aprende a caminar de forma constante adaptando continuamente sus acciones para lograr el objetivo de avanzar sin caerse. Este proceso de aprendizaje por ensayo y error es la esencia del aprendizaje por refuerzo (AR). Todos los animales aprenden de sus experiencias de interacción con el entorno y ajustan su comportamiento para lograr los resultados deseados.
Inspirado por este concepto, el aprendizaje automático en la inteligencia artificial permite a las máquinas interactuar con su entorno y aprender el comportamiento óptimo a partir de la experiencia. Es una de las ramas más apasionantes del aprendizaje automático (y también una de las más desafiantes). En 2016, DeepMind de Google desarrolló AlphaGo, un agente de IA que ganó contra el campeón mundial en el juego de Go, un juego de mesa de estrategia abstracta conocido por su complejidad. AlphaGo aprendió a jugar a un nivel sobrehumano no imitando movimientos expertos, sino jugando millones de partidas contra sí mismo. Muchos consideran que este es un logro histórico que mostró el poder del aprendizaje automático para resolver problemas que alguna vez se consideraron exclusivamente humanos.
A pesar del entusiasmo que rodea al RL, los recursos sobre el tema pueden ser limitados y muy difíciles de seguir, lo que lo hace inaccesible para muchos. En este artículo, mi objetivo es proporcionar una humilde introducción al RL, cubriendo los conceptos básicos de sus fundamentos matemáticos e ilustrando una configuración a través de un ejemplo; enseñando a un agente a operar de manera óptima una planta de energía simplificada. Actualmente estoy aprendiendo y trabajando con RL, por lo que gran parte del trabajo aquí serán mis notas condensadas.
Introducción al aprendizaje por refuerzo
El núcleo del aprendizaje por refuerzo consiste en entrenar a un agente para que tome una decisión o una secuencia de decisiones dentro de un entorno para maximizar su recompensa acumulativa. A diferencia del aprendizaje supervisado, en el que se proporciona la salida etiquetada correcta para cada entrada, el aprendizaje por refuerzo se basa en que el agente aprenda de las consecuencias de sus acciones, es decir, que aprenda esencialmente de la experiencia. Antes de sumergirnos en las matemáticas, describamos los componentes/conceptos clave dentro de un marco de aprendizaje por refuerzo:
- Agente : El que toma las decisiones.
- Entorno : El sistema con el que el agente interactúa para determinar las consecuencias de sus acciones.
- Estado(s) : Una representación de una situación dentro del entorno.
- Acción (a) : Un conjunto de todas las acciones posibles que el agente puede realizar
- Recompensa (r) : Retorno inmediato recibido después de la transición de un estado; es decir, el retorno de realizar una acción.
- Política (π) : La estrategia que utilizará el agente para determinar la próxima acción en función del estado actual.
Este marco también se demuestra esquemáticamente en esta imagen:

El proceso de decisión de Markov (MDP)
Para formular problemas de aprendizaje por refuerzo, se utiliza el proceso de decisión de Markov (MDP). Un MDP proporciona un modelo matemático para la toma de decisiones, donde los resultados son en parte aleatorios y en parte bajo el control del que toma las decisiones (agente).
Un proceso de decisión de Markov se define por (S,A,P,R,γ), donde:
- S: Un conjunto de estados.
- A: Un conjunto de acciones.
- P(s′∣s,a): La probabilidad de transición del estado s al estado s′ después de la acción a.
- R(s,a): La recompensa esperada recibida después de realizar la acción a en el estado s.
- γ ∈[0,1] : El factor de descuento; equilibra las recompensas inmediatas y futuras. Un valor cercano a 0 hace que el agente sea miope (priorizando las recompensas inmediatas), mientras que un valor cercano a 1 alienta al agente a considerar las recompensas a largo plazo.
La propiedad de Markov es un supuesto clave en los MDP que establece que el estado futuro depende únicamente del estado actual y de la acción realizada, no del historial de estados y acciones que lo precedieron. Esta propiedad “sin memoria” simplifica el diseño de algoritmos de RL.
Objetivo: maximizar la recompensa acumulada
El objetivo/propósito del agente es encontrar una política óptima π* que maximice la recompensa acumulada esperada a lo largo del tiempo. La política asigna estados a acciones, π: S→A, y determina la acción que realizará el agente en cada estado dado.
La recompensa/rendimiento acumulativo se define como la suma de las recompensas futuras descontadas:

· Gt: retorno en el paso de tiempo t.
· r_(t+k+1): Recompensa recibida en el paso de tiempo t+k+1.
· γ: Factor de descuento (0≤γ≤1).
Funciones de valor
Para tomar decisiones, el agente estima el valor de los estados y las acciones. Las funciones de valor cuantifican lo bueno que es para el agente estar en un estado determinado y realizar una acción determinada en ese estado determinado.
Función estado-valor:
La función de valor de estado, V^π(s), es el rendimiento esperado cuando se parte del estado s y se sigue la política π para todos los estados subsiguientes o se escribe matemáticamente como:

Esta función cuantifica el valor a largo plazo de estar en el estado actual bajo la política π.
Función Acción-Valor:
La función de valor de acción Q^π(s, a) es el rendimiento esperado después de tomar la acción a en el estado s y posteriormente seguir la política π para todos los estados restantes:

Esta función cuantifica el valor de realizar la acción a en el estado actual s bajo la política π.
La ecuación de Bellman
Estas funciones de valor son recursivas, donde el valor de cualquier estado o acción es esencialmente la recompensa por la acción inmediata seguida del valor del nuevo estado. Estas relaciones recursivas se conocen como ecuaciones de Bellman.
Ecuación de Bellman para la función estado-valor (V^π (s)):

Para cada acción posible que el agente puede tomar en el estado s, ponderada por la probabilidad π(a∣s) de tomar esa acción bajo la política π:
· Recompensa inmediata: R(s,a) es la recompensa esperada por realizar la acción a en el estado s
· Valor futuro: γ∑P(s′∣s,a)V^π(s′) es el valor descontado del siguiente estado s′, ponderado por la probabilidad P(s′∣s,a) de transición a s′
En términos simples, esta ecuación esencialmente dice que el valor del estado 𝑠 es la recompensa inmediata esperada más el valor descontado esperado del próximo estado, considerando todas las acciones y transiciones posibles.
Política óptima y funciones de valor
Una política óptima π* produce el valor más alto para todos los estados:

De manera similar, la función acción-valor óptima es:

El objetivo de la mayoría de los algoritmos de RL es encontrar Q*(s,a) o V*(s), que luego definen la política óptima. Por ejemplo, una política óptima determinista puede ser que, para cualquier estado dado, el agente seleccione la acción que tenga la función de valor de acción máxima:

Pero, claramente, podemos adoptar dos enfoques diferentes: optimizar las funciones de valor de estado y acción u optimizar la política parametrizada directamente. Analizaremos brevemente ambos enfoques.
Función-valor: aprendizaje de diferencias temporales
Al igual que el entrenamiento normal de redes neuronales con retropropagación después de cada lote, el RL también necesita actualizar las funciones de valor en función de las consecuencias de las acciones tomadas. Según la naturaleza del problema en cuestión, existen diferentes enfoques para esto. Un enfoque popular es el aprendizaje de diferencia temporal (TD), que se puede utilizar tanto en tareas episódicas (con un estado inicial y terminal claros) como en tareas continuas (sin un estado terminal). TD actualiza las estimaciones de valor después de cada paso. El aprendizaje de TD actualiza las estimaciones de valor en función de la diferencia entre las recompensas previstas y las reales. Esto se puede escribir como

· r_t+1: Recompensa recibida después de realizar la acción A_t en el estado S_t.
· V(S_t+1): Valor estimado del siguiente estado.
· V(S_t): Estimación actual del valor del estado S_t
El error TD δt mide la diferencia entre el valor esperado y el valor observado del estado actual. La regla de actualización para la función de valor es:

donde α es la tasa de aprendizaje. La estimación del valor V(S_t) se actualiza en función de la recompensa observada más el valor descontado del siguiente estado. Este método permite al agente aprender funciones de valor directamente de la experiencia sin procesar sin un modelo del entorno.
Métodos de gradiente de políticas
Mientras que los métodos basados en el valor se centran en la estimación de funciones de valor, el objetivo de los métodos de gradiente de políticas es optimizar directamente la política parametrizada. La política está parametrizada por θ y el objetivo es maximizar el rendimiento esperado:

Luego, los parámetros de la política se actualizan utilizando el método estándar de descenso de gradiente (aquí estamos maximizando, por lo que en realidad es un método de ascenso de gradiente):

Pero calcular ∇_θ J(θ) es complicado. Dado que J(θ) implica una expectativa sobre todas las posibles secuencias de acciones, no es sencillo calcularlo directamente. Aquí es donde el Teorema del Gradiente de Política proporciona una forma práctica de calcular este gradiente:

El término ∇_θlnπ_θ(a∣s) es el gradiente de la probabilidad logarítmica de tomar la acción a en el estado s bajo la política π_θ. Esta ecuación significa que los parámetros de la política se ajustan para aumentar la probabilidad de acciones que conduzcan a mayores recompensas.
Optimización de políticas proximales (PPO)
En la práctica, se utilizan métodos como la Optimización de Políticas Proximales (PPO) para estabilizar el entrenamiento y mejorar el rendimiento. La función objetivo de la PPO es:

Donde r_t (θ) es la relación de probabilidad entre las políticas nuevas y antiguas:

Ā es la estimación de la ventaja en el momento t, que mide cuánto mejor es la acción a_t en comparación con la acción promedio en el estado s_t. ϵ es un hiperparámetro que controla el rango de recorte. La función de recorte garantiza que la actualización no se desvíe demasiado de la política anterior, lo que ayuda a mantener un aprendizaje estable. Este objetivo sustituto recortado evita esencialmente grandes actualizaciones que podrían desestabilizar el entrenamiento.
La función de ventaja Ā_t representa cuánto mejor es una acción en comparación con el promedio. Se calcula de la siguiente manera:

- Si Ā_t>0, la acción es mejor de lo esperado y la política debería aumentar su probabilidad.
- Si Ā_t <0, la acción es peor de lo esperado y la política debería disminuir su probabilidad.
Aplicación del aprendizaje automático a las operaciones de las centrales eléctricas
Con una comprensión básica del aprendizaje por refuerzo y sus fundamentos matemáticos, apliquemos el aprendizaje por refuerzo para enseñar a un agente a operar de manera óptima una planta de energía. La operación de una planta de energía implica tomar decisiones que equilibren múltiples objetivos, como la seguridad, satisfacer la demanda de energía, minimizar los costos operativos, cumplir con las regulaciones de emisiones y programar el mantenimiento. Entiendo que esto es una simplificación excesiva y enorme del funcionamiento de una planta de energía, pero esto solo pretende ser un ejemplo simple para demostrar el aprendizaje por refuerzo.
Definición del entorno
Los estados (s) son una combinación de factores externos y estados internos. El estado s_t incluye:
- Factores externos:
- Previsión de la demanda (d_t )
- Precios del combustible (p_carbón,t; p_gas,t)
- Parámetros de eficiencia (e_caldera,t e_turbina,t)
- Otras variables externas; una lista se muestra en la siguiente figura.
- Estados internos:
- Potencia de salida (P_t)
- Tasa de consumo de combustible (F_t)
- Niveles de emisiones (E_t)
- Estado de mantenimiento (M_t)
- Niveles de almacenamiento de energía (S_t)
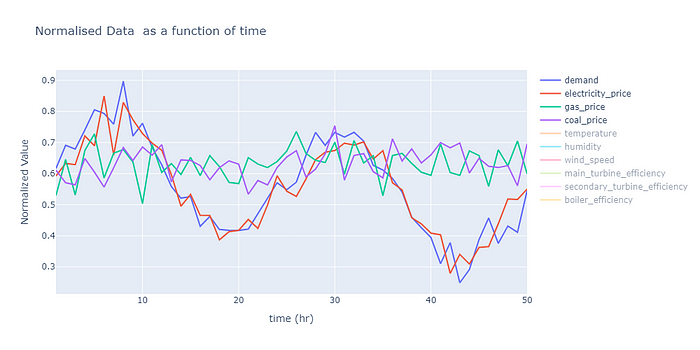
Las variables externas son datos sintéticos. En la imagen siguiente se muestran algunos ejemplos de estas variables. El código para la generación de datos sintéticos se generó para encapsular el comportamiento estacional de estas variables en el mundo real por hora del día y época del año. No incluiré el código aquí, pero es bastante sencillo de leer y se puede acceder a él en GitHub.

Las acciones (a) son las variables de control, como las salidas de la turbina, las relaciones de mezcla de combustible y los ajustes de control de emisiones. La lista de acciones en el momento t incluye:
- Salida de la turbina principal (a1,t)
- Salida de la turbina secundaria (a2,t)
- Relación de mezcla de combustible (a3,t)
- Nivel de excitación del generador (a4,t)
- Intensidad de control de emisiones (a5,t)
Estas acciones son variables continuas delimitadas por límites operacionales.
Comencemos a escribir el código del entorno. Usaremos la biblioteca Gymnasium para crear nuestro entorno ‘gym’. Esta parte del código solo contiene la inicialización de todos los parámetros de la clase, que también son los parámetros utilizados al comienzo de la ejecución.
importar gimnasio como gimnasio
desde gimnasio importar espacios
importar numpy como np
importar pandas como pd
desde pydantic importar Campo, BaseModel, ConfigDict
desde src.utils.logger importar logger
desde escribiendo importar Dict , Lista
clase EnvironmentConfig ( BaseModel ):
Datos: pd.DataFrame = Campo(..., descripción= "Datos de entrada de factores externos" )
lista_acciones: Dict = Campo(..., descripción= "lista de posibles acciones que se pueden tomar" )
valor_inicial_estados_internos: Dict = Campo(..., descripción= "todos los estados internos" )
variables_entorno: Dict = Campo(..., descripción= "cualquier otra variable que no esté incluida en los estados internos o externos" )
configuración_modelo = ConfigDict(tipos_arbitrarios_permitidos= Verdadero )
clase TheEnvironment (gym.Env):
def __init__ ( self, config:EnvironmentConfig ):
super (ElEntorno, self).__init__()
self.config = config
# número de características
self.external_conds_data = config.Data
self.ExternalDfeatures = len (self.external_conds_data.columns)
# Variables del entorno
self.EnvironVariables = config.environment_varibales
# DEFINICIÓN DEL ESPACIO DE ACCIÓN Y LOS ESPACIOS DE OBSERVACIÓN:
acciones_posibles = config.lista_acciones
Número_acciones = len (acciones_posibles)
self.espacio_acción = espacios.Box(
bajo= 0 ,alto= 1 ,
forma=(Número_acciones,),
dtype = np.float32
)
self.valor_inicial_estados_internos = config.valor_inicial_estados_internos
self.forma_obs = self.ExternalDfeatures + len (self.valor_inicial_estados_internos)
self.observation_space = spaces.Box(
low = -np.inf,
high = np.inf,
shape = (self.obs_shape,), dtype = np.float32
)
Inicialización de #current_stuep
self.current_step = 0
self.max_steps = len (self.external_conds_data)- 1
# inicialización de estados internos
self.current_power_output = self.internal_states_initial_value[ 'potencia_de_salida_actual' ]
self.fuel_consumption_rate = self.internal_states_initial_value[ 'tasa_de_consumo_de_combustible' ]
self.emissions_levels = self.internal_states_initial_value[ 'niveles_de_emisiones' ]
self.current_operating_costs = self.internal_states_initial_value [ 'costos_operativos_actuales' ] self.emissions_quota = self.internal_states_initial_value[ 'cuota_de_emisiones ' ] self.hours_main_turbine_since_maintenance = self.internal_states_initial_value[ 'horas_turbina_principal_desde_mantenimiento' ] self.horas_turbina_secundaria_desde_mantenimiento = self.valor_inicial_estados_internos[ 'horas_turbina_secundaria_desde_mantenimiento' ] # INICIALIZACIÓN DE ACCIONES self.relación_mezcla_combustible_actual = self.valor_inicial_estados_internos[ 'relación_mezcla_combustible_actual' ] # Variables de entorno: self.Main_turbineOffCount = 0 self.SecondTurbineOffCount = 0 self.EnergyStorage = self.valor_inicial_estados_internos[ 'Almacenamiento_inicial' ] self.Total_reward = 0
Mapeo de la acción al estado
Para evaluar las acciones de los agentes de RL y mapear correctamente las transiciones de estado, necesitamos definir un modelo. Este modelo podrá predecir o mapear las acciones a los siguientes estados. El entorno pasa al siguiente estado s_(t+1) en función del estado y la acción actuales:

donde f representa la parte determinista de la dinámica del entorno (es decir, el modelo) y ϵ_t representa las variaciones estocásticas. Por ejemplo, el estado interno, la salida de potencia (P_t) se puede definir en términos de las acciones de la siguiente manera:

Hemos definido una relación similar entre todas las acciones y estados internos.
Continuando con el código anterior, la función ObservationSpace toma una instantánea del estado actual; coloca todas las variables externas en el paso actual, así como las variables internas, como la salida de energía actual y la cantidad de energía almacenada, etc., en una lista que será utilizada por el agente para predecir las acciones a tomar.
def ObservationSpace ( self ):
"""obteniendo el estado actual del entorno"""
observation_frame = []
# DATOS EXTERNOS
para variable en self.external_conds_data.columns:
df = self.external_conds_data[variable]
min_val = min (df)
max_val = max (df)
mean_val = np.mean(df)
if self.current_step < len (df):
# print(f"column: {variable}, value: {df.iloc[self.current_step]}, type: {type(df.iloc[self.current_step])}")
para_scaled = (df.iloc[self.current_step]-mean_val)/(max_val-min_val)
# si el paso actual es más largo que el marco de datos
# entonces agrega los últimos datos dados
else :
para_scaled = (df.iloc[- 1 ]-mean_val)/(max_val-min_val)
observation_frame.append(df.iloc[- 1 ])
# ESTADOS INTERNOS
# estos están escalados aproximadamente por ahora pero deben hacerse correctamente más tarde
observation_frame.append(self.current_power_output/ 400 )
observation_frame.append(self.fuel_consumption_rate/ 400 )
observation_frame.append(self.current_fuel_mixture_ratio)
observation_frame.append(self.emissions_levels/ 500 )
observation_frame.append(self.current_operating_costs/ 1000 )
observation_frame.append(self.emissions_quota/ 6000 )
observation_frame.append(self.hours_main_turbine_since_maintenance/ 10 )
observation_frame.append(self.hours_secondary_turbine_since_maintenance/ 10 )
marco_de_observación.append(self.EnergyStorage/ 6000 )
return np.array(marco_de_observación)
Ahora definimos la función de paso que, dado un conjunto de acciones del agente, tomará un solo paso de esas acciones para observar la consecuencia de las acciones, es decir, la recompensa. También calculará todos los estados internos y el espacio de observación (del código anterior) que se utilizarán para calcular el siguiente conjunto de acciones.
def step ( self, acciones ):
self.current_step += 1
# comprobar si el número de pasos ya es superior al número máximo de pasos permitidos
done = self.current_step >= self.max_steps
if done:
recompensa, recompensa acumulada = self.RewardCalculation()
return self.ObservationSpace(), recompensa, done, False , {}
# observación, recompensa, done, información
# Todas las acciones
self.main_turbine_output = (acciones[ 0 ]+ self.config.actions_list[ 'main_turbine_output' ][ 0 ])*self.config.actions_list [ 'main_turbine_output ' ][ 1 ]
self.secondary_turbine_output = (acciones[ 1 ]+ self.config.actions_list[ 'secondary_turbine_output' ][ 0 ])*self.config.actions_list[ 'secondary_turbine_output' ][ 1 ]
self.current_fuel_mixture_ratio = (acciones[ 2 ]+ self.config.actions_list[ 'current_fuel_mixture_ratio' ][ 0 ])*self.config.actions_list[ 'current_fuel_mixture_ratio' ][ 1 ]
self.generator_excitation = (acciones[ 3 ]+ self.config.actions_list[ 'generator_excitation' ][ 0 ])*self.config.actions_list[ 'generator_excitation' ][ 1 ]
self.emissions_control_intensity = (acciones[ 4 ]+ self.config.actions_list[ 'emissions_control_intensity' ][ 0 ])*self.config.actions_list[ 'emissions_control_intensity' ][ 1 ]
# Calcular los estados internos resultantes:
self.CalculateInternalStates()
observación = self.ObservationSpace()
recompensa, accum_reward = self.RewardCalculation()
info = {
"diferencia_de_potencia" : self.demanda_de_potencia_actual - self.salida_de_potencia_actual,
"cuota_de_emisiones" : self.cuota_de_emisiones,
"almacenamiento_de_energía" : self.Almacenamiento_de_energía,
"recompensa" : recompensa
}
return observación, recompensa, hecho, Falso , info # Falso es para truncado
Dado el espacio de observación, el agente determina un conjunto de acciones que, a su vez, determinan el estado. Para representar el efecto de las acciones en la variable de estados internos, se define una función CalculateInternalStates para actualizar los estados internos después de que se realiza un paso. Estas actualizaciones se definen en función de reglas simples de conservación.
# código de entorno para la transición de estado
def CalculateInternalStates ( self ):
# Potencia de salida
main_T_eff = self.external_conds_data [ ' eficiencia_de_la_turbina_principal' ].iloc[self.current_step]
second_T_eff = self.external_conds_data[ 'eficiencia_de_la_turbina_secundaria' ].iloc[self.current_step]
potencia_base = self.salida_de_la_turbina_principal*main_T_eff + self.salida_de_la_turbina_secundaria*second_T_eff
potencia_generada = potencia_base*self.excitación_del_generador
if self.current_step < self.max_steps:
# print(f"paso actual: {self.current_step}, pasos máximos: {self.max_steps}, longitud de los datos: {len(self.external_conds_data['demanda'])}")
potencia_demanda = self.external_conds_data[ 'demanda' ].iloc[self.current_step+ 1 ]
else :
demanda_de_potencia = self.external_conds_data[ 'demanda' ].iloc[- 1 ]
# el excedente va al almacenamiento y el déficit se compensa con el almacenamiento
self.current_power_demand = demanda_de_potencia
diferencia_de_potencia = potencia_generada - demanda_de_potencia
# almacenamiento
capacidad_de_almacenamiento = self.EnvironVariables[ 'capacidad_de_almacenamiento_de_energía' ]
if diferencia_de_potencia >= 0 :
if self.EnergyStorage < capacidad_de_almacenamiento:
self.EnergyStorage += diferencia_de_potencia
self.current_power_output = demanda_de_potencia
else :
if self.EnergyStorage+diferencia_de_potencia >= 0 : # es decir, en realidad queda suficiente
self.EnergyStorage -= diferencia_de_potencia
self.current_power_output = demanda_de_potencia
else : # es decir, no queda suficiente en el almacenamiento
self.current_power_output = self.EnergyStorage + power_generated
self.EnergyStorage = 0
# Consumo de combustible
boiler_eff = self.external_conds_data[ 'boiler_efficiency' ].iloc[self.current_step]
power_generated = self.main_turbine_output+self.secondary_turbine_output
consumo_gas = power_generated*( 1 -self.current_fuel_mixture_ratio)/ boiler_eff
consumo_carbón = power_generated*self.current_fuel_mixture_ratio/boiler_eff
self.fuel_consumption_rate = consumo_gas+consumo_carbón
# Emisiones
base_emissions = self.fuel_consumption_rate * (
self.current_fuel_mixture_ratio* 2 +
( 1 -self.current_fuel_mixture_ratio))
self.emissions_levels = base_emissions*( 1 -self.emissions_control_intensity/ 100 )
self.emissions_quota -= self.emissions_levels
if self.current_step % ( 24 * 28 ) == 0 : # es decir, cada 4 semanas se reinicia la cuota de emisiones
self.emissions_quota = self.internal_states_initial_value[ 'emissions_quota' ]
# costos operativos
precio_carbón = self.external_conds_data[ 'coal_price' ].iloc[self.current_step]
precio_gas = self.external_conds_data[ 'gas_price' ].iloc[self.current_step]
self.current_operating_costs = self.fuel_consumption_rate*(
self.current_fuel_mixture_ratio*coal_price +
( 1 -self.current_fuel_mixture_ratio)*gas_price)
# actualiza los tiempos de funcionamiento de la turbina
si self.main_turbine_output > 0 :
self.hours_main_turbine_since_maintenance += 1
# tiempo de mantenimiento requerido
tiempo_de_mantenimiento = self.EnvironVariables[ 'Tiempo_de_mantenimiento_de_la_turbina' ]
si self.main_turbine_output == 0 :
self.Main_turbineOffCount += 1
si self.Main_turbineOffCount >= tiempo_de_mantenimiento:
self.hours_main_turbine_since_maintenance = 0
self.Main_turbineOffCount = 0
si self.secondary_turbine_output > 0 :
self.hours_secondary_turbine_since_maintenance += 1
si self.secondary_turbine_output == 0 :
self.SecondTurbineOffCount += 1
si self.SecondTurbineOffCount >= tiempo_de_mantenimiento:
self.horas_turbina_secundaria_desde_mantenimiento = 0
self.SecondTurbineOffCount = 0
Función de recompensa
Definamos una función de recompensa que encapsule los objetivos operativos que incluyen la satisfacción de la demanda de energía, los costos operativos, los costos de emisiones, los costos de mantenimiento y los costos de control de emisiones.
Para la demanda de potencia, podemos penalizar cualquier desviación de la demanda:

Costos operativos, solo incluiremos los costos de consumo de combustible:

Donde F es el consumo de combustible y el superíndice es la fuente de combustible. Costes de emisiones, penalizando al modelo si el nivel de emisiones supera las cuotas:

Para evitar que el modelo utilice algún instrumento durante un tiempo prolongado sin mantenimiento, podemos añadir un término penalizador:

Costo de emplear medidas de control de emisiones:

Todos estos se pueden combinar para definir la función de recompensa que encapsula todos los diferentes objetos:

Todas estas ecuaciones se definen en el código de la siguiente manera.
def RewardCalculation ( self ):
# Asegurar el cumplimiento de la demanda de potencia
power_difference = self.current_power_demand - self.current_power_output
# Mantenimiento de turbinas:
Turbine_use_limit = self.EnvironVariables[ 'Turbine_use_b4_maintenance' ]
# Turbina principal
si self.hours_main_turbine_since_maintenance > Turbine_use_limit:
outstanding_maintenance_MT = np.exp(self.hours_main_turbine_since_maintenance - Turbine_use_limit)
de lo contrario :
outstanding_maintenance_MT = 0
# Turbina secundaria
si self.hours_secondary_turbine_since_maintenance > Turbine_use_limit:
outstanding_maintenance_ST = np.exp(self.hours_secondary_turbine_since_maintenance - Turbine_use_limit)
de lo contrario :
outstanding_maintenance_ST = 0
# REUNIÓN CUOTA DE EMISIÓN
si self.emissions_quota < 0 :
extra_emission = -self.emissions_quota
de lo contrario :
extra_emission = 0
# costos asociados con el control de emisiones
emission_control_costs = self.emissions_control_intensity* 1000 *np.exp(self.emissions_control_intensity)
# incluidos los costos operativos y de combustible
electrical_price = self.external_conds_data[ 'electricity_price' ].iloc[self.current_step]
recompensa = ( 5 *self.current_power_output*electricity_price -
self.current_operating_costs - power_difference* 1000 -
outstanding_maintenance_MT * 20000 - outstanding_maintenance_ST* 20000 -
extra_emission * 5 -
emission_control_costs)
self.current_step_reward = recompensa/ 1e6 # recompensa escalada para estabilidad numérica
self.Total_reward += self.current_step_reward
devolver recompensa, self.Total_reward
Definiendo al Agente
Ahora podemos comenzar a definir el agente con la biblioteca stable_baseline3. El agente se define como parte de una clase general con varias funciones que permiten entrenar al agente, utilizarlo para realizar predicciones de inferencia y también ejecutarlo en los datos de validación para verificar si hay sobreajustes durante el entrenamiento.
clase AgentConfig ( BaseModel ):
total_timesteps: int = Field(..., description= "número total de pasos" )
entorno: DummyVecEnv = Field(..., description= "Entorno para que se ejecute el agente" )
validación_timesteps: int = Field(..., description= "Número de pasos para la validación" )
tren_timesteps: int = Field(default= 100 , description= "¡SOLO PARA PRUEBAS! SE UTILIZA PARA CARGAR EL MODELO GUARDADO" )
model_config = ConfigDict(arbitrary_types_allowed= True )
clase PPOAgent :
def __init__ ( self, config: AgentConfig ):
self.callback = PolicyGradientLossCallback()
self.Agent = PPO(
"MlpPolicy" ,
config.environment,
verbose = 1 ,
learning_rate= 1e-5 ,
gamma= 0.99 ) # tamaño_lote=256
self.config = config
def train ( self ):
self.Agent.learn(total_timesteps=self.config.total_timesteps, callback = self.callback)
logger.info( "Entrenamiento finalizado" )
def predict ( self, observación ):
acción,_ = self.Agent.predict(observación)
return acción
def validar ( self ):
entorno = self.config.environment
observación = entorno.reset()
Recompensas = []
recompensas_acum = 0
recompensa_acumulable = np.zeros(self.config.validation_timesteps)
para ii en rango (self.config.validation_timesteps):
acciones, _ = self.Agent.predict(observación)
observación, recompensa, hecho, _ = entorno.step(acciones) # Desempaquetando solo 4, aunque se devuelve 5 - problema con la versión actual de DummyVecEnv
Recompensas.append(recompensa)
recompensas_acumuladas += recompensa
recompensa_acumulada[ii] = recompensas_acumuladas
# comprobar si la simulación está completa
si se hace:
observación = entorno.reset()
print ( f"Recompensa acumulativa al final de{self.config.validation_timesteps} pasos de validación: {accumulative_reward[- 1 ]} " )
logger.info( f"Recompensa acumulativa al final de {self.config.validation_timesteps} pasos de validación: {accumulative_reward[- 1 ]} " )
return np.array(Rewards), accumulative_reward
Entrenando al agente
Ahora podemos entrenar y probar el agente. El código para las funciones de entrenamiento y prueba es muy similar: consiste en reunir el código del agente anterior y el entorno definido y entrenarlo para una cantidad predefinida de pasos, seguidos de la validación o prueba del agente.
clase ModelEvaluationConfig ( BaseModel ):
# Rutas de datos
training_data_path: str = Field(default= "data/processed/train.csv" , description= "ruta a los datos de entrenamiento" )
val_data_path: str = Field(default= "data/processed/val.csv" , description= "ruta a los datos de validación" )
test_data_path: str = Field(default= "data/processed/test.csv" , description= "ruta a los datos de prueba" )
# Variables de entorno del agente
agent_possible_actions: Dict = Field(..., description= "todas las acciones posibles y rango de valores" )
train_total_timesteps: int = Field(default= 20000 , description= "número total de pasos durante el entrenamiento" )
validation_timesteps: int = Field(default= 300 , description= "Número de pasos para la validación" )
test_timesteps: int = Field(default= 300 ,description= "Número de pasos durante la prueba" )
# Variables de entorno:
internalStates_InitialVal: dict = Field(..., description= "un diccionario de todos los estados internos y su valor inicial" )
environment_variables: dict = Field(..., description= "un diccionario de cualquier otra variable de entorno" )
# Carga del agente entrenado previamente durante la prueba
use_pretrained_agent: bool = Field(default= True , description = "si es verdadero, cargará el agente entrenado previamente antes de la prueba" )
model_config=ConfigDict(arbitrary_types_allowed= True )
class Model_train :
def __init__ ( self, config:ModelEvaluationConfig ):
self.config = config
def train_agent ( self ):
## ENTRENAMIENTO
#datos de entrenamiento
train_data = pd.read_csv(Path(self.config.training_data_path))
# Crear configuración de entorno
env_config = EnvironmentConfig(
Datos=datos_de_entrenamiento,
lista_de_acciones=self.config.agent_posibles_acciones,
valor_inicial_de_estados_internos=self.config.internalStates_InitialVal,
variables_entorno=self.config.variables_entorno
)
entorno_entrenamiento = DummyVecEnv([ lambda : TheEnvironment(env_config)])
configuración_agente = AgentConfig(pasos_de_tiempo_totales=self.config.pasos_de_tiempo_totales_entrenamiento,
entorno=entorno_entrenamiento,
pasos_de_tiempo_validación=self.config.pasos_de_tiempo_validación
)
agente = PPOAgent(configuración_agente)
# entrenamiento del agente:
agente.entrenamiento()
# VALIDACIÓN DEL AGENTE
val_data = pd.read_csv(Path(self.config.val_data_path))
val_env_config = EnvironmentConfig(
Datos=val_data,
lista_de_acciones=self.config.agent_possible_actions,
valor_inicial_estados_internos=self.config.valor_inicial_estados_internos,
variables_entorno=self.config.variables_entorno
)
val_environment = DummyVecEnv([ lambda : TheEnvironment(val_env_config)])
# evaluar el agente
Reward, accumulative_reward = agent.validate()
# guardar el agente entrenado:
agent.save_trained_agent()
return train_environment, val_environment, agente, Reward, accumulative_reward
def test_agent ( self ):
test_data = pd.read_csv(Path(self.config.test_data_path))
# Crear configuración del entorno
env_config = EnvironmentConfig(
Data=test_data,
action_list=self.config.agent_possible_actions,
internal_states_initialValue=self.config.internalStates_InitialVal,
environment_varibales=self.config.environment_variables
)
test_environment = DummyVecEnv([ lambda : El entorno(env_config)])
agent_config = AgentConfig(total_timesteps=self.config.test_timesteps,
entorno=test_environment,
validation_timesteps=self.config.validation_timesteps,
train_timesteps=self.config.train_total_timesteps
)
agente = PPOAgent(agent_config)
# cargar agente preentrenado
si self.config.use_pretrained_agent:
agente.load_trained_agent()
recompensa_acumulada = np.zeros(self.config.test_timesteps)
Recompensas = np.zeros(self.config.test_timesteps)
accum_reward_perstep = 0
espacio_de_observación = []
obs = entorno_de_prueba.reset()
para ii en el rango (self.config.test_timesteps):
acción = agente.predict(obs)
obs, recompensa, hecho, información = entorno_de_prueba.step(acción)
Recompensas[ii] = recompensa
accum_reward_perstep += recompensa
accum_reward[ii] = accum_reward_perstep
espacio_de_observación.append(obs)
si se hace:
obs = entorno_de_prueba.reset()
devolver accum_reward,Recompensas, espacio_de_observación
El código completo y el pipeline están disponibles en github . Podemos probar la capacidad de los agentes para operar con datos de prueba utilizando un agente entrenado solo para 10k pasos como línea base y comparándolo con el rendimiento de un agente entrenado para 500k pasos. A continuación, se muestra una imagen de la recompensa acumulada que muestra una diferencia significativa. El agente entrenado solo para 10k pasos también puede realizar acciones aleatorias, la recompensa acumulada disminuye cada vez más. Mientras que un agente entrenado para 500k pasos ha aprendido a operar para aumentar la recompensa acumulada de modo que la central eléctrica funcione con ganancias y no con pérdidas.

A pesar de la falta de ajuste de los hiperparámetros del modelo, en realidad ha hecho un trabajo decente; podríamos ajustar aún más el modelo para obtener un mejor rendimiento.
Esto nos lleva al final de este artículo. El aprendizaje por refuerzo es una de las ramas más apasionantes y menos desarrolladas de la IA. Será muy interesante ver los avances de este campo, pero también su aplicación a diferentes problemas. Por último, gracias por tomarte el tiempo de leer este artículo. Espero que te haya resultado útil para comprender el aprendizaje por refuerzo o su contexto matemático. Este artículo es solo una humilde introducción, hay mucho más que leer sobre los conceptos fundamentales que sustentan el aprendizaje por refuerzo.
Todas las imágenes son del autor.