Predicción de datos de series temporales con aprendizaje automático, inteligencia artificial generativa y aprendizaje profundo.

Palash Mishra, 19 de junio de 2024. MEDIUM

Ingeniero FullStack experimentado y entusiasta del aprendizaje automático con pasión por desarrollar productos web innovadores y optimizar soluciones ML.

La predicción de datos de series temporales es un aspecto fundamental en diversas industrias, desde las finanzas y la atención médica hasta el marketing y la logística. La capacidad de pronosticar valores futuros en función de datos históricos puede impulsar mejoras significativas en los procesos de toma de decisiones y la eficiencia operativa. Con los avances en el aprendizaje automático, la inteligencia artificial generativa y el aprendizaje profundo, ahora hay métodos más sofisticados disponibles para abordar los problemas de predicción de series temporales. En este blog, exploraremos diferentes enfoques y modelos que se pueden utilizar para la predicción de datos de series temporales.

Comprensión de los datos de series temporales

Los datos de series temporales son una secuencia de puntos de datos recopilados o registrados en intervalos de tiempo específicos. Algunos ejemplos son los precios de las acciones, los datos meteorológicos, las cifras de ventas y las lecturas de los sensores. El objetivo de la predicción de series temporales es utilizar observaciones pasadas para predecir valores futuros, lo que puede resultar complicado debido a las complejidades y patrones inherentes a los datos.

1. Enfoques de aprendizaje automático

1.1 ARIMA (Media móvil autorregresiva integrada)

ARIMA es un método estadístico clásico para la previsión de series temporales. Combina modelos autorregresivos (AR), modelos de diferenciación (para que los datos sean estacionarios) y modelos de promedio móvil (MA).

Ejemplo de uso:importar pandas como pd
desde statsmodels.tsa.arima.model importar ARIMA

# Cargar los datos de la serie temporal
time_series_data = pd.read_csv( ‘time_series_data.csv’ )
time_series_data[ ‘Fecha’ ] = pd.to_datetime(time_series_data[ ‘Fecha’ ])
time_series_data.set_index( ‘Fecha’ , inplace= True )

# Ajustar
el modelo ARIMA model = ARIMA(time_series_data[ ‘Valor’ ], order=( 5 , 1 , 0 )) # (p,d,q)
model_fit = model.fit()

# Hacer predicciones
predictions = model_fit.forecast(steps= 10 )
print (predicciones)

1.2 SARIMA (ARIMA estacional)

SARIMA amplía ARIMA al tener en cuenta los efectos estacionales. Resulta útil para datos con patrones estacionales, como los datos de ventas mensuales.

Ejemplo de uso:importar pandas como pd
importar numpy como np
desde statsmodels.tsa.statespace.sarimax importar SARIMAX

# Ajustar
el modelo SARIMA model = SARIMAX(time_series_data[ ‘Valor’ ], order=( 1 , 1 , 1 ), seasonal_order=( 1 , 1 , 1 , 12 )) # (p,d,q) (P,D,Q,s)
model_fit = model.fit(disp= False )

# Hacer predicciones
predictions = model_fit.forecast(steps= 10 )
imprimir (predicciones)

1.3 Profeta

Desarrollado por Facebook, Prophet es una poderosa herramienta diseñada para pronosticar datos de series de tiempo que puede manejar datos faltantes y valores atípicos y proporcionar intervalos de incertidumbre confiables.

Ejemplo de uso:de fbprophet import Prophet
import pandas como pd

# Ajustar el modelo de Prophet
model = Prophet()
model.fit(time_series_data)

# Crear un marco de datos y predicciones futuras
future = model.make_future_dataframe(periods= 10 )
forecast = model.predict(future)
print (forecast[[ ‘ds’ , ‘yhat’ , ‘yhat_lower’ , ‘yhat_upper’ ]])

1.4 XGBoost

XGBoost es un marco de potenciación de gradiente que se puede utilizar para la predicción de series de tiempo transformando el problema en una tarea de aprendizaje supervisado, tratando los pasos de tiempo anteriores como características.

Ejemplo de uso:importar pandas como pd
importar numpy como np
desde xgboost importar XGBRegressor
desde sklearn.model_selection importar train_test_split
desde sklearn.metrics importar mean_squared_error

# Cargar los datos de series temporales
time_series_data = pd.read_csv( ‘time_series_data.csv’ )
time_series_data[ ‘Fecha’ ] = pd.to_datetime(time_series_data[ ‘Fecha’ ])
time_series_data.set_index( ‘Fecha’ , inplace= True )

# Preparar los datos para el aprendizaje supervisado
def create_lag_features ( data, lag= 1 ):
df = data.copy()
for i in range ( 1 , lag + 1 ):
df[ f’lag_ {i} ‘ ] = df[ ‘Valor’ ].shift(i)
return df.dropna()

lag = 5
data_with_lags = create_lag_features(time_series_data, lag=lag)
X = data_with_lags.drop( ‘Value’ , axis= 1 )
y = data_with_lags[ ‘Value’ ]

# Dividir los datos en conjuntos de entrenamiento y prueba
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size= 0.2 , shuffle= False )

# Ajustar
el modelo XGBoost model = XGBRegressor(objective= ‘reg:squarederror’ , n_estimators= 1000 )
model.fit(X_train, y_train)

# Hacer predicciones
y_pred = model.predict(X_test)
mse = mean_squared_error(y_test, y_pred)
print ( f’Error cuadrático medio: {mse} ‘ )

2. Enfoques de IA generativa

2.1 GAN (Redes generativas antagónicas)

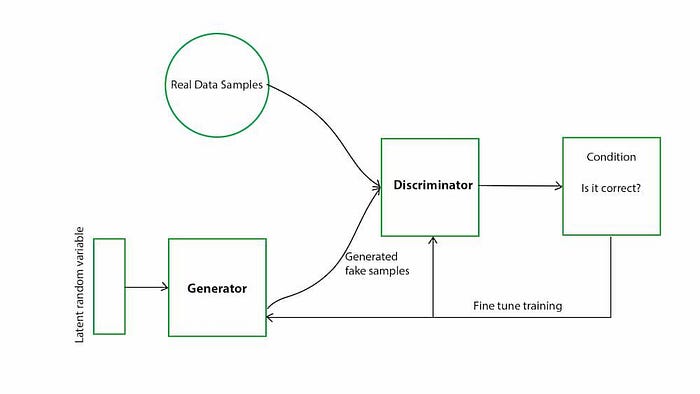
Las GAN constan de un generador y un discriminador. Para la predicción de series temporales, las GAN pueden generar secuencias futuras plausibles mediante el aprendizaje de la distribución de datos subyacente.

Ejemplo de uso:importar numpy como np
importar pandas como pd
desde tensorflow.keras.models importar Sequential
desde tensorflow.keras.layers importar Dense, LSTM, Conv1D, MaxPooling1D, Flatten, LeakyReLU, Reshape
desde tensorflow.keras.optimizers importar Adam

# Preparar los datos para GAN
def create_dataset ( dataset, time_step= 1 ):
X, Y = [], []
para i en rango ( len (dataset)-time_step- 1 ):
a = conjunto_de_datos[i:(i+paso_de_tiempo), 0 ]
X.append(a)
Y.append(conjunto_de_datos[i + paso_de_tiempo, 0 ])
return np.array(X), np.array(Y)

paso_de_tiempo = 10
escalador = MinMaxScaler(rango_de_características=( 0 , 1 ))
datos_escalados = escalador.fit_transform(datos_de_serie_temporal[ ‘Valor’ ].values.reshape(- 1 , 1 ))

tren_X, tren_y = crear_conjunto_de_datos(datos_escalados, paso_de_tiempo)
tren_X = tren_X.reshape(tren_X.shape[ 0 ], tren_X.shape[ 1 ], 1 )

# Componentes GAN
def build_generator ():
modelo = Sequential()
modelo.add(Dense( 100 , input_dim=paso_de_tiempo))
model.add(LeakyReLU(alpha= 0.2 ))
model.add(Dense(time_step, activation= ‘tanh’ ))
model.add(Reshape((time_step, 1 )))
return model

def build_discriminator ():
model = Sequential()
model.add(LSTM( 50 , input_shape=(time_step, 1 )))
model.add(Dense( 1 , activation= ‘sigmoid’ ))
return model

# Construye y compila el discriminador discriminator
= build_discriminator()
discriminator.compile (loss= ‘binary_crossentropy’ , optimized=Adam( 0.0002 , 0.5 ), metrics=[ ‘accuracy’ ])

# Construye el
generador generator = build_generator()

# El generador toma ruido como entrada y genera datos
z = Input(shape=(time_step,))
generated_data = generator(z)

# Para el modelo combinado, solo entrenaremos al generador
discriminator.trainable = False

# El discriminador toma datos generados como entrada y determina la validez validation
= discriminator(generated_data)

# El modelo combinado (generador apilado y discriminador)
combined = Model(z, validation)
combined. compile (loss= ‘binary_crossentropy’ , optimized=Adam( 0.0002 , 0.5 ))

# Entrenando la GAN
epochs = 10000
batch_size = 32
valid = np.ones((batch_size, 1 ))
fake = np.zeros((batch_size, 1 ))

para epoch en el rango (epochs):
# ———————
# Entrenar discriminador
# ———————

# Seleccionar un lote aleatorio de datos reales
idx = np.random.randint( 0 , X_train.shape[ 0 ], batch_size)
real_data = X_train[idx]

# Generar un lote de datos falsos
noise = np.random.normal( 0 , 1 , (batch_size, time_step))
gen_data = generator.predict(noise)

# Entrenar al discriminador
d_loss_real = discriminator.train_on_batch(real_data, valid)
d_loss_fake = discriminator.train_on_batch(gen_data, fake)
d_loss = 0.5 * np.add(d_loss_real, d_loss_fake)

# ———————
# Entrenar generador
# ———————

noise = np.random.normal( 0 , 1 , (batch_size, time_step))

# Entrenar el generador (para que el discriminador etiquete las muestras como válidas)
g_loss = combined.train_on_batch(noise, valid)

# Imprimir el progreso
si época % 1000 == 0 :
print ( f» {epoch} [D loss: {d_loss[ 0 ]} | D accurate: { 100 *d_loss[ 1 ]} ] [G loss: {g_loss} ]»)

# Hacer predicciones
noise = np.random.normal( 0 , 1 , ( 1 , time_step))
predicción_generada = generador.predict(ruido)
predicción_generada = escalar.inverse_transform(predicción_generada)
print (predicción_generada)

2.2 Red de ondas

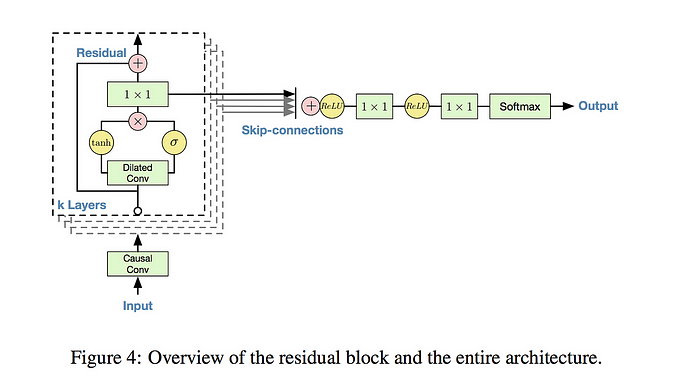
Desarrollado por DeepMind, WaveNet es un modelo generativo profundo diseñado originalmente para la generación de audio, pero que ha sido adaptado para la previsión de series de tiempo, especialmente en el dominio del audio y el habla.

Ejemplo de uso:importar numpy como np
importar pandas como pd
importar tensorflow como tf
desde sklearn.preprocessing importar MinMaxScaler
desde tensorflow.keras.models importar Model
desde tensorflow.keras.layers importar Input, Conv1D, Add, Activation, Multiply, Lambda, Dense, Flatten
desde tensorflow.keras.optimizers importar Adam

# Preparar los datos para WaveNet
scaler = MinMaxScaler(feature_range=( 0 , 1 ))
scaled_data = scaler.fit_transform(datos_de_serie_temporal[ ‘Valor’ ].values.reshape(- 1 , 1 ))

def create_dataset ( conjunto_de_datos, paso_de_tiempo= 1 ):
X, Y = [], []
para i en rango ( len (conjunto_de_datos)-paso_de_tiempo- 1 ):
a = conjunto_de_datos[i:(i+paso_de_tiempo), 0 ]
X.append(a)
Y.append(conjunto_de_datos[i + paso_de_tiempo, 0 ])
return np.array(X), np.array(Y)

paso_de_tiempo = 10
X, y = create_dataset(datos_escalados, paso_de_tiempo)
X = X.reshape(X.shape[ 0 ], X.shape[ 1 ], 1 )

# Definir el modelo WaveNet
def residual_block ( x, tasa_de_dilatación ):
tanh_out = Conv1D( 32 , tamaño_del_núcleo= 2 , tasa_de_dilatación=tasa_de_dilatación, relleno= ‘causal’ , activación= ‘tanh’ )(x)
sigm_out = Conv1D( 32 , tamaño_del_núcleo= 2 , tasa_de_dilatación=tasa_de_dilatación, relleno= ‘causal’ , activación= ‘sigmoide’ )(x)
salida = Multiplicar()([tanh_out, sigm_out])
salida = Conv1D( 32 , tamaño_del_núcleo= 1 , relleno= ‘igual’ )(salida)
salida = Sumar()([salida, x])
devolverfuera

capa_de_entrada = Entrada(forma=(paso_de_tiempo, 1 ))
fuera = Conv1D( 32 , tamaño_del_núcleo= 2 , relleno= ‘causal’ , activación= ‘tanh’ )(capa_de_entrada)
saltar_conexiones = []
para i en rango ( 10 ):
fuera = bloque_residual(fuera, 2 **i)
saltar_conexiones.append(fuera)

fuera = Agregar()(salir_conexiones)
fuera = Activación( ‘relu’ )(fuera)
fuera = Conv1D( 1 , tamaño_del_núcleo= 1 , activación= ‘relu’ )(fuera)
fuera = Aplanar()(fuera)
fuera = Denso( 1 )(fuera)

modelo = Modelo(capa_de_entrada, fuera)
modelo. compile (optimizer=Adam(learning_rate= 0.001 ), loss= ‘mean_squared_error’ )

# Entrenar el modelo
model.fit(X, y, epochs= 10 , batch_size= 16 )

# Hacer predicciones
predictions = model.predict(X)
predictions = scaler.inverse_transform(predictions)
print (predictions)

3. Enfoques de aprendizaje profundo

3.1 LSTM (Memoria a Largo Plazo y Corto Plazo)

Las redes LSTM son un tipo de red neuronal recurrente (RNN) capaz de aprender dependencias a largo plazo. Se utilizan ampliamente para la predicción de series temporales debido a su capacidad para capturar patrones temporales.

Ejemplo de uso:importar numpy como np
importar pandas como pd
desde tensorflow.keras.models importar Sequential
desde tensorflow.keras.layers importar LSTM, Dense
desde sklearn.preprocessing importar MinMaxScaler

# Preparar los datos para LSTM
scaler = MinMaxScaler(feature_range=( 0 , 1 ))
scaled_data = scaler.fit_transform(time_series_data[ ‘Valor’ ].values.reshape(- 1 , 1 ))

train_size = int ( len (datos_escalados) * 0.8 )
datos_de_entrenamiento = datos_escalados[:tamaño_de_entrenamiento]
datos_de_prueba = datos_escalados[tamaño_de_entrenamiento:]

def crear_conjunto_de_datos ( conjunto_de_datos, paso_de_tiempo= 1 ):
X, Y = [], []
para i en rango ( longitud (conjunto_de_datos)-paso_de_tiempo- 1 ):
a = conjunto_de_datos[i:(i+paso_de_tiempo), 0 ]
X.append(a)
Y.append(conjunto_de_datos[i + paso_de_tiempo, 0 ])
return np.array(X), np.array(Y)

paso_de_tiempo = 10
X_entrenamiento, y_entrenamiento = crear_conjunto_de_datos(datos_de_entrenamiento, paso_de_tiempo)
X_prueba, y_prueba = crear_conjunto_de_datos(datos_de_prueba, paso_de_tiempo)

X_entrenamiento = X_entrenamiento.reshape(X_entrenamiento.shape[ 0 ], X_entrenamiento.shape[ 1 ], 1 )
X_prueba = X_test.reshape(X_test.shape[ 0 ], X_test.shape[ 1 ], 1 )

# Construir el modelo LSTM
model = Sequential()
model.add(LSTM( 50 , return_sequences= True , input_shape=(time_step, 1 )))
model.add(LSTM( 50 , return_sequences= False ))
model.add(Dense( 25 ))
model.add(Dense( 1 ))

model.compila (optimizador= ‘adam’ , pérdida= ‘ error_cuadrático_medio’ )
model.fit(X_train, y_train, tamaño_lote= 1 , épocas= 1 )

# Hacer predicciones
train_predict = model.predict(X_train)
test_predict = model.predict(X_test)

train_predict = scaler.inverse_transform(train_predict)
test_predict = scaler.inverse_transform(test_predict)
print (test_predict)

3.2 GRU (Unidad recurrente cerrada)

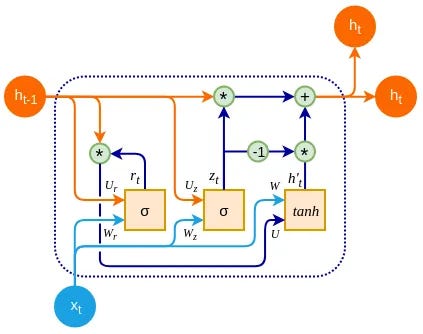
GRU es una variante de LSTM que es más simple y suele funcionar igual de bien para tareas de series temporales. Los GRU se utilizan para modelar secuencias y capturar dependencias temporales.

Ejemplo de uso:importar numpy como np
importar pandas como pd
desde tensorflow.keras.models importar Sequential
desde tensorflow.keras.layers importar GRU, Dense
desde sklearn.preprocessing importar MinMaxScaler

# Preparar los datos para GRU
scaler = MinMaxScaler(feature_range=( 0 , 1 ))
scaled_data = scaler.fit_transform(time_series_data[ ‘Valor’ ].values.reshape(- 1 , 1 ))

train_size = int ( len (datos_escalados) * 0.8 )
datos_de_entrenamiento = datos_escalados[:tamaño_de_entrenamiento]
datos_de_prueba = datos_escalados[tamaño_de_entrenamiento:]

paso_de_tiempo = 10
X_entrenamiento, y_entrenamiento = crear_conjunto_de_datos(datos_de_entrenamiento, paso_de_tiempo)
X_prueba, y_prueba = crear_conjunto_de_datos(datos_de_prueba, paso_de_tiempo)

X_entrenamiento = X_entrenamiento.reshape(X_entrenamiento.shape[ 0 ], X_entrenamiento.shape[ 1 ], 1 )
X_prueba = X_test.reshape(X_test.shape[ 0 ], X_test.shape[ 1 ], 1 )

# Construir modelo GRU
model = Sequential()
model.add(GRU( 50 , return_sequences= True , input_shape=(time_step, 1 )))
model.add(GRU( 50 , return_sequences= False ))
model.add(Dense( 25 ))
model.add(Dense( 1 ))

model.compila (optimizador= ‘adam’ , pérdida= ‘ error_cuadrático_medio’ )
model.fit(X_train, y_train, tamaño_lote= 1 , épocas= 1 )

# Hacer predicciones
train_predict = model.predict(X_train)
test_predict = model.predict(X_test)

train_predict = scaler.inverse_transform(train_predict)
test_predict = scaler.inverse_transform(test_predict)
print (test_predict)

3.3 Modelos de transformadores

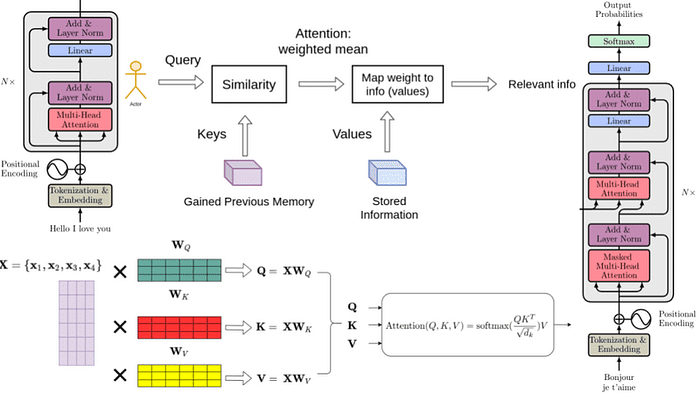
Los transformadores, conocidos por su éxito en las tareas de procesamiento del lenguaje natural, se han adaptado para la predicción de series temporales. Los modelos como el Transformador de Fusión Temporal (TFT) aprovechan el mecanismo de atención para manejar datos temporales de manera eficaz.

Ejemplo de uso:importar numpy como np
importar pandas como pd
desde sklearn.preprocessing importar MinMaxScaler
desde tensorflow.keras.models importar Sequential
desde tensorflow.keras.layers importar Dense, LSTM, Conv1D, MaxPooling1D, Flatten, MultiHeadAttention, LayerNormalization, Dropout

# Cargue sus datos de series de tiempo
time_series_data = pd.read_csv( ‘time_series_data.csv’ )
time_series_data[ ‘Fecha’ ] = pd.to_datetime(time_series_data[ ‘Fecha’ ])
time_series_data.set_index( ‘Fecha’ , inplace= True )

# Prepare los datos
scaler = MinMaxScaler(feature_range=( 0 , 1 ))
scaled_data = scaler.fit_transform(time_series_data[ ‘Valor’ ].values.reshape(- 1 , 1 ))

tamaño_entrenamiento = int ( len (datos_escalados) * 0.8 )
datos_entrenamiento = datos_escalados[:tamaño_entrenamiento]
datos_prueba = datos_escalados[tamaño_entrenamiento:]

def crear_conjunto_datos ( conjunto_datos, paso_tiempo= 1 ):
X, Y = [], []
para i en rango ( len (conjunto_datos)-paso_tiempo- 1 ):
a = conjunto_datos[i:(i+paso_tiempo), 0 ]
X.append(a)
Y.append(conjunto_datos[i + paso_tiempo, 0 ])
return np.array(X), np.array(Y)

paso_tiempo = 10
X_entrenamiento, y_entrenamiento = crear_conjunto_datos(datos_entrenamiento, paso_tiempo)
X_prueba, y_prueba = crear_conjunto_datos(datos_prueba, paso_tiempo)

X_entrenamiento = X_train.reshape(X_train.shape[ 0 ], X_train.shape[ 1 ], 1 )
X_test = X_test.reshape(X_test.shape[ 0 ], X_test.shape[ 1 ], 1 )

# Construir modelo de transformador
modelo = Sequential()
modelo.add(MultiHeadAttention(num_heads= 4 , key_dim= 2 , input_shape=(time_step, 1 )))
modelo.add(LayerNormalization())
modelo.add(Dense( 50 , activation= ‘relu’ ))
modelo.add(Dropout( 0.1 ))
modelo.add(Dense( 1 ))

modelo.compilar (optimizador= ‘adam’ , pérdida= ‘error_cuadrático_medio’ )
modelo.ajuste(entrenamiento_X, entrenamiento_y, tamaño_lote= 1 , épocas= 1 )

# Hacer predicciones
entrenar_predicción = modelo.predicción(entrenamiento_X)
probar_predicción = modelo.predicción(prueba_X)

entrenar_predicción = escalador.transformación_inversa(entrenar_predicción)
probar_predicción = escalador.transformación_inversa(probar_predicción)
imprimir (probar_predicción)

3.4 Seq2Seq (Secuencia a secuencia)

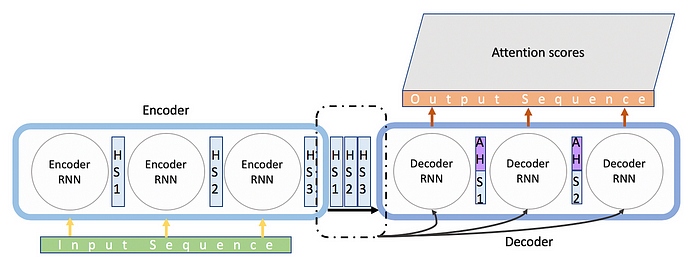
Los modelos Seq2Seq se utilizan para predecir secuencias de datos. Originalmente desarrollados para la traducción de idiomas, son eficaces para la predicción de series temporales al aprender la correspondencia entre secuencias de entrada y secuencias de salida.

Ejemplo de uso:importar numpy como np
importar pandas como pd
desde tensorflow.keras.models importar Model
desde tensorflow.keras.layers importar Input, LSTM, Dense

# Cargar los datos de la serie temporal
time_series_data = pd.read_csv( ‘time_series_data.csv’ )
time_series_data[ ‘Date’ ] = pd.to_datetime(time_series_data[ ‘Date’ ])
time_series_data.set_index( ‘Date’ , inplace= True )

# Preparar los datos para Seq2Seq
def create_dataset ( dataset, time_step= 1 ):
X, Y = [], []
para i en rango ( len (dataset)-time_step- 1 ):
a = dataset[i:(i+time_step), 0 ]
X.append(a)
Y.append(dataset[i + time_step, 0 ]
) np.array(X), np.array(Y)

paso_de_tiempo = 10
escalador = MinMaxScaler(rango_de_características=( 0 , 1 ))
datos_escalados = escalador.fit_transform(datos_de_serie_temporal[ ‘Valor’ ].values.reshape(- 1 , 1 ))

X, y = crear_conjunto_de_datos(datos_escalados, paso_de_tiempo)
X = X.reshape(X.shape[ 0 ], X.shape[ 1 ], 1 )

# Definir el modelo Seq2Seq
entradas_del_codificador = Entrada(forma=(paso_de_tiempo, 1 ))
codificador = LSTM( 50 , estado_de_retorno= True )
salidas_del_codificador, estado_h, estado_c = codificador(entradas_del_codificador)

entradas_del_decodificador = Entrada(forma=(paso_de_tiempo, 1 ))
decoder_lstm = LSTM( 50 , return_sequences= True , return_state= True )
decoder_outputs, _, _ = decoder_lstm(decoder_inputs, initial_state=[state_h, state_c])
decoder_dense = Dense( 1 )
decoder_outputs = decoder_dense(decoder_outputs)

model = Model([encoder_inputs, decoder_inputs], decoder_outputs)
model.compila (optimizador= ‘adam’ , pérdida= ‘error_cuadrado_medio’ ) # Entrenar el modelo model.fit([X, X], y, épocas= 10 , tamaño_lote= 16 ) # Hacer predicciones

predicciones = model.predict([X, X])
predicciones = scaler.inverse_transform(predicciones)
print (predicciones)

3.5 TCN (Redes convolucionales temporales)

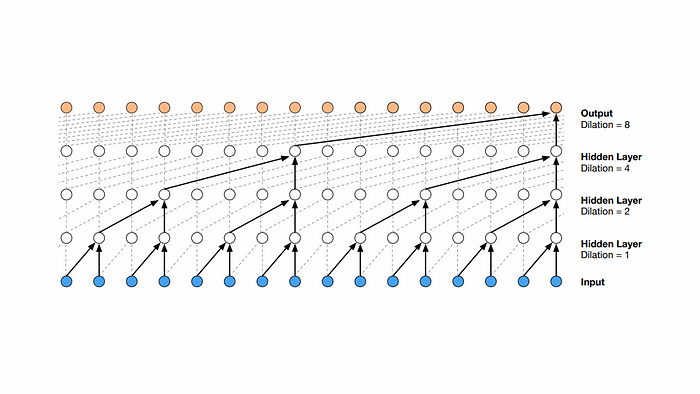
Las TCN utilizan convoluciones dilatadas para capturar dependencias a largo plazo en datos de series temporales. Ofrecen una alternativa sólida a las RNN para el modelado de datos secuenciales.

# Preparar los datos para TCN
def create_dataset ( dataset, time_step= 1 ):
X, Y = [], []
para i en rango ( len (dataset)-time_step- 1 ):
a = dataset[i:(i+time_step), 0 ]
X.append(a)
Y.append(conjunto_de_datos[i + paso_de_tiempo, 0 ])
return np.array(X), np.array(Y)

paso_de_tiempo = 10
escalador = MinMaxScaler(rango_de_características=( 0 , 1 ))
datos_escalados = escalador.fit_transform(datos_de_serie_temporal[ ‘Valor’ ].values.reshape(- 1 , 1 ))

X, y = crear_conjunto_de_datos(datos_escalados, paso_de_tiempo)
X = X.reshape(X.shape[ 0 ], X.shape[ 1 ], 1 )

# Definir el modelo TCN modelo
= Sequential()
modelo.add(Conv1D(filtros= 64 , tamaño_de_núcleo= 2 , tasa_de_dilatación= 1 , activación= ‘relu’ , forma_de_entrada=(paso_de_tiempo, 1 )))
modelo.add(Conv1D(filtros= 64 , tamaño_del_núcleo= 2 , tasa_de_dilatación= 2 , activación= ‘relu’ ))
model.add(Conv1D(filtros= 64 , tamaño_del_núcleo= 2 , tasa_de_dilatación= 4 , activación= ‘relu’ ))
model.add(Flatten()) model.add
(Dense( 1 ))

model.compila (optimizador= ‘adam’ , pérdida= ‘error_cuadrado_medio’ ) # Entrena el modelo model.fit(X, y, épocas= 10 , tamaño_del_lote= 16

)

# Hacer predicciones
predicciones = model.predict(X)
predicciones = scaler.inverse_transform(predicciones)
print (predicciones)

3.6 AR profunda

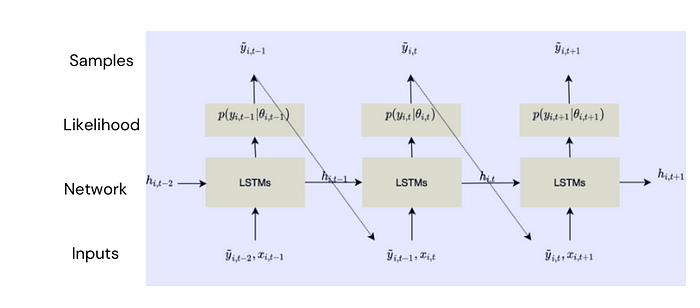
DeepAR, desarrollada por Amazon, es una red autorregresiva recurrente diseñada para la previsión de series temporales. Maneja múltiples series temporales y puede capturar patrones complejos.

# Preparar los datos para el modelo tipo DeepAR
def create_dataset ( dataset, time_step= 1 ):
X, Y = [], []
para i en rango ( len (dataset)-time_step- 1 ):
a = dataset[i:(i+time_step), 0 ]
X.append(a)
Y.append(conjunto de datos[i + paso_de_tiempo, 0 ])
return np.array(X), np.array(Y)

paso_de_tiempo = 10
escalador = MinMaxScaler(rango_de_características=( 0 , 1 ))
datos_escalados = escalador.fit_transform(datos_de_serie_temporal[ ‘Valor’ ].values.reshape(- 1 , 1 ))

X, y = crear_conjunto_de_datos(datos_escalados, paso_de_tiempo)
X = X.reshape(X.shape[ 0 ], X.shape[ 1 ], 1 )

# Definir un modelo similar a DeepAR
modelo = Sequential()
modelo.add(LSTM( 50 , return_sequences= True , input_shape=(paso_de_tiempo, 1 )))
modelo.add(LSTM( 50 ))
modelo.add(Dense( 1 ))

modelo. compile (optimizer= ‘adam’ , loss= ‘mean_squared_error’ )

# Entrena el modelo
model.fit(X, y, epochs= 10 , batch_size= 16 )

# Haz predicciones
predictions = model.predict(X)
predictions = scaler.inverse_transform(predictions)
print (predictions)

La predicción de series temporales es un campo complejo pero fascinante que se beneficia enormemente de los avances en aprendizaje automático, inteligencia artificial generativa y aprendizaje profundo. Al aprovechar modelos como ARIMA, Prophet, LSTM y Transformers, los profesionales pueden descubrir patrones ocultos en los datos y hacer pronósticos precisos. A medida que la tecnología continúa evolucionando, las herramientas y los métodos disponibles para la predicción de series temporales se volverán cada vez más sofisticados, lo que ofrecerá nuevas oportunidades de innovación y mejora en varios dominios.

Predicción de datos de series temporales con aprendizaje automático, inteligencia artificial generativa y aprendizaje profundo.

Comprensión de los datos de series temporales

1. Enfoques de aprendizaje automático

2. Enfoques de IA generativa

3. Enfoques de aprendizaje profundo

Comparte en tus perfiles

Artículos Relacionados:

Se publica el Informe sobre Desarrollo Humano 2025

Bienestar y felicidad.

El curriculum y la persona.