Uso de árboles de decisión para una segmentación rápida

Mariya Mansurov. 26 de mayo de 2025

Al trabajar con productos, podríamos vernos en la necesidad de introducir algunas «reglas». Permítanme explicar a qué me refiero con «reglas» con ejemplos prácticos:
- Imaginemos que estamos viendo una ola masiva de fraude en nuestro producto y queremos restringir la incorporación de un segmento específico de clientes para reducir este riesgo. Por ejemplo, descubrimos que la mayoría de los estafadores tenían agentes de usuario y direcciones IP específicos de ciertos países.
- Otra opción es enviar cupones a nuestros clientes para que los usen en nuestra tienda online. Sin embargo, nos gustaría atender solo a los clientes con probabilidad de abandono, ya que los usuarios fieles volverán al producto de todos modos. Podríamos determinar que el grupo más viable son los clientes que se unieron hace menos de un año y redujeron su gasto en más del 30 % el mes pasado.
- Las empresas transaccionales suelen tener un segmento de clientes con pérdidas. Por ejemplo, un cliente de un banco pasó la verificación y contactó regularmente con atención al cliente (lo que generó costos de alta y servicio) mientras que prácticamente no realizó transacciones (por lo que no generó ingresos). El banco podría implementar una pequeña cuota de suscripción mensual para los clientes con menos de 1000 $ en su cuenta, ya que probablemente no sean rentables.
Por supuesto, en todos estos casos, podríamos haber utilizado un modelo complejo de aprendizaje automático que considerara todos los factores y predijera la probabilidad (ya sea de que un cliente sea un estafador o abandone la cuenta). Aun así, en algunas circunstancias, podríamos preferir un conjunto de reglas estáticas por las siguientes razones:
- La velocidad y complejidad de la implementación. Implementar un modelo de aprendizaje automático en producción requiere tiempo y esfuerzo. Si actualmente experimenta una ola de fraude, podría ser más viable implementar un conjunto de reglas estáticas rápidamente y luego desarrollar una solución integral.
- Interpretabilidad. Los modelos de aprendizaje automático son como cajas negras. Aunque podamos comprender a grandes rasgos su funcionamiento y cuáles son sus características más importantes, resulta complicado explicárselos a los clientes. En el ejemplo de las cuotas de suscripción para clientes sin fines de lucro, es importante compartir un conjunto de reglas transparentes con los clientes para que puedan comprender los precios.
- Cumplimiento. Algunos sectores, como el financiero o el sanitario, podrían requerir decisiones auditables y basadas en normas para cumplir con los requisitos de cumplimiento.
En este artículo, quiero mostrarles cómo podemos resolver problemas empresariales utilizando estas reglas. Tomaremos un ejemplo práctico y profundizaremos en este tema:
- Discutiremos qué modelos podemos usar para extraer dichas reglas de los datos.
- Construiremos un clasificador de árbol de decisiones desde cero para aprender cómo funciona,
- Ajustaremos el
sklearnmodelo Clasificador de Árbol de Decisión para extraer las reglas de los datos, - Aprenderemos a analizar la estructura del árbol de decisión para obtener los segmentos resultantes.
- Finalmente, exploraremos diferentes opciones para la codificación de categorías, ya que la
sklearnimplementación no admite variables categóricas.
Tenemos muchos temas que cubrir, así que vamos a ello.
Caso
Como siempre, es más fácil aprender algo con un ejemplo práctico. Así que, comencemos analizando la tarea que resolveremos en este artículo.
Trabajaremos con el conjunto de datos de Marketing Bancario . Este conjunto de datos contiene información sobre las campañas de marketing directo de una entidad bancaria portuguesa. De cada cliente, conocemos diversas características y si contrató un depósito a plazo fijo (nuestro público objetivo).
Nuestro objetivo comercial es maximizar el número de conversiones (suscripciones) con recursos operativos limitados. Por lo tanto, no podemos contactar a toda nuestra base de usuarios y queremos obtener el mejor resultado con los recursos disponibles.
El primer paso es revisar los datos. Carguemos el conjunto de datos.
importar pandas como pd
pd.set_option( 'display.max_colwidth' , 5000 )
pd.set_option( 'display.float_format' , lambda x: '%.2f' % x)
df = pd.read_csv( 'bank-full.csv' , sep = ';' )
df = df.drop([ 'duration' , 'campaign' ], axis = 1 )
# Se eliminaron las columnas relacionadas con la campaña de marketing actual,
# ya que introducen fugas de datos
df.head()
Sabemos bastante sobre los clientes, incluidos datos personales (como el tipo de trabajo o el estado civil) y su comportamiento anterior (por ejemplo, si tienen un préstamo o su saldo anual promedio).

El siguiente paso es seleccionar un modelo de aprendizaje automático. Existen dos clases de modelos que se suelen utilizar cuando necesitamos algo fácilmente interpretable:
- árboles de decisión,
- regresión lineal o logística.
Ambas opciones son viables y pueden generar buenos modelos fáciles de implementar e interpretar. Sin embargo, en este artículo, me gustaría centrarme en el modelo de árbol de decisión, ya que genera reglas reales, mientras que la regresión logística nos dará la probabilidad como una suma ponderada de características.
Preprocesamiento de datos
Como hemos visto en los datos, hay muchas variables categóricas (como la educación o el estado civil). Desafortunadamente, la sklearnimplementación del árbol de decisión no admite datos categóricos, por lo que necesitamos preprocesarlos.
Comencemos transformando los indicadores sí/no en números enteros.
para p en [ 'predeterminado' , 'vivienda' , 'préstamo' , 'y' ]:
df [p] = df [p].map(lambda x: 1 si x == 'sí' de lo contrario 0)
El siguiente paso es transformar la monthvariable. Podemos usar la codificación one-hot para los meses, introduciendo indicadores como month_jan, month_feb, etc. Sin embargo, podría haber efectos estacionales, y creo que sería más razonable convertir los meses a enteros siguiendo su orden.
month_map = {
'jan' : 1 , 'feb' : 2 , 'mar' : 3 , 'apr' : 4 , 'may' : 5 , 'jun' : 6 ,
'jul' : 7 , 'ago' : 8 , 'sep' : 9 , 'oct' : 10 , 'nov' : 11 , 'dic' : 12
}
# Ahorré 5 minutos al pedirle a ChatGPT que hiciera este mapeo df
[ 'month' ] = df.month.map ( lambda x: month_map[x] if x in month_map else x)
Para todas las demás variables categóricas, utilicemos la codificación one-hot. Más adelante analizaremos diferentes estrategias de codificación de categorías, pero por ahora, nos ceñiremos al enfoque predeterminado.
La forma más fácil de realizar codificación one-hot es aprovechar get_dummies la función en pandas.
fin_df = pd.get_dummies(
df, columnas=[ 'trabajo' , 'marital' , 'educación' , 'resultado' , 'contacto' ],
dtype = int , # para convertir a indicadores 0/1
drop_first = False # para mantener todos los valores posibles
)
Esta función transforma cada variable categórica en una columna 1/0 independiente para cada posible valor. Podemos ver cómo funciona para poutcomela columna.
fin_df.merge(df [['id', 'resultado']] )\
.groupby([ 'resultado' , 'resultado_desconocido' , 'resultado_fallido' ,
'resultado_otro' , 'resultado_éxito' ], as_index = False).y.count()\ .rename
( columnas = { 'y' : 'casos' })\ .sort_values( 'casos' , ascendente = False)

Nuestros datos ya están listos y es hora de analizar cómo funcionan los clasificadores de árboles de decisión.
Clasificador de árboles de decisión: teoría
En esta sección, exploraremos la teoría del clasificador de árbol de decisión y desarrollaremos el algoritmo desde cero. Si le interesa más un ejemplo práctico, puede pasar a la siguiente parte.
La forma más sencilla de comprender el modelo de árbol de decisión es con un ejemplo. Construyamos un modelo simple basado en nuestros datos. Usaremos DecisionTreeClassifier de sklearn.
nombres_de_características = fin_df.drop([ 'y' ], eje = 1 ).columnas
modelo = sklearn.tree.DecisionTreeClassifier(
profundidad_máxima = 2 , muestras_mínimas_hoja = 1000 )
modelo.fit(fin_df[nombres_de_características], fin_df[ 'y' ])
El siguiente paso es visualizar el árbol.
dot_data = sklearn.tree.export_graphviz(
model, out_file= None , feature_names = feature_names,filled = True ,
percentage = True , precision = 2
# para mostrar las porciones de clases en lugar de números absolutos
)
graph = graphviz.Source(dot_data)
graph

Así pues, podemos ver que el modelo es sencillo. Se trata de un conjunto de divisiones binarias que podemos usar como heurística.
Veamos cómo funciona el clasificador internamente. Como siempre, la mejor manera de comprender el modelo es construir la lógica desde cero.
La piedra angular de cualquier problema es la función de optimización. Por defecto, en el clasificador de árbol de decisión, optimizamos el coeficiente de Gini . Imaginemos que obtenemos un elemento aleatorio de la muestra y luego el otro. El coeficiente de Gini equivaldría a la probabilidad de que estos elementos pertenezcan a clases diferentes. Por lo tanto, nuestro objetivo será minimizar el coeficiente de Gini.
En el caso de solo dos clases (como en nuestro ejemplo, donde la intervención de marketing tuvo éxito o no), el coeficiente de Gini se define únicamente por un parámetro p, donde pes la probabilidad de obtener un artículo de una de las clases. La fórmula es la siguiente:

Si nuestra clasificación es ideal y somos capaces de separar perfectamente las clases, entonces el coeficiente de Gini será igual a 0. El peor escenario es cuando p = 0.5, entonces el coeficiente de Gini también será igual a 0,5.
Con la fórmula anterior, podemos calcular el coeficiente de Gini para cada hoja del árbol. Para calcular el coeficiente de Gini de todo el árbol, necesitamos combinar los coeficientes de Gini de las divisiones binarias. Para ello, podemos obtener una suma ponderada:

Ahora que sabemos qué valor estamos optimizando, solo necesitamos definir todas las divisiones binarias posibles, iterar sobre ellas y elegir la mejor opción.
Definir todas las posibles divisiones binarias también es bastante sencillo. Podemos hacerlo una por una para cada parámetro, ordenar los posibles valores y establecer umbrales entre ellos. Por ejemplo, para meses (número entero del 1 al 12).

Intentemos codificarlo y veamos si obtenemos el mismo resultado. Primero, definiremos funciones que calculen el coeficiente de Gini para un conjunto de datos y su combinación.
def get_gini ( df ):
p = df.y.mean()
return 2 *p*( 1 -p)
print (get_gini(fin_df))
# 0.2065
# cerca de lo que vemos en el nodo raíz del árbol de decisión
def get_gini_comb ( df1, df2 ):
n1 = df1.shape[ 0 ]
n2 = df2.shape[ 0 ]
gini1 = get_gini(df1)
gini2 = get_gini(df2)
return (gini1*n1 + gini2*n2)/(n1 + n2)
El siguiente paso es obtener todos los umbrales posibles para un parámetro y calcular sus coeficientes de Gini.
importar tqdm
def optimizar_un_parámetro ( df, parámetro ):
tmp = []
valores_posibles = lista ( ordenado (df[parámetro].unique()))
imprimir (parámetro)
para i en tqdm.tqdm( rango ( 1 , len (valores_posibles))):
umbral = (valores_posibles[i- 1 ] + valores_posibles[i])/ 2
gini = obtener_gini_comb(df[df[parámetro] <= umbral],
df[df[parámetro] > umbral])
tmp.append(
{ 'parámetro' : parámetro,
'umbral' : umbral,
'gini' : gini,
'tamaños' : (df[df[parámetro] <= umbral].forma[ 0 ], df[df[parámetro] > umbral].forma[ 0 ]))
}
)
devolver pd.DataFrame(tmp)
El paso final es iterar a través de todas las características y calcular todas las divisiones posibles.
tmp_dfs = []
para la función en nombres_de_funciones:
tmp_dfs.append(optimizar_un_parámetro(fin_df, función))
opt_df = pd.concat(tmp_dfs)
opt_df.sort_values( 'gini' , asceding = True).head ( 5)

¡Genial! Obtuvimos el mismo resultado que en nuestro DecisionTreeClassifiermodelo. La distribución óptima es si se aplica poutcome = successo no. Hemos reducido el coeficiente de Gini de 0,2065 a 0,1872.
Para continuar construyendo el árbol, necesitamos repetir el proceso recursivamente. Por ejemplo, bajando por la poutcome_success <= 0.5rama:
tmp_dfs = []
para la función en nombres_de_funciones:
tmp_dfs.append(optimizar_un_parámetro(
fin_df[fin_df.poutcome_success <= 0.5], función))
opt_df = pd.concat(tmp_dfs)
opt_df.sort_values( 'gini' , ascendente = Verdadero).head ( 5)

La única cuestión que aún nos queda por resolver son los criterios de parada. En nuestro ejemplo inicial, usamos dos condiciones:
max_depth = 2— simplemente limita la profundidad máxima del árbol,min_samples_leaf = 1000Nos impide obtener nodos hoja con menos de 1K muestras. Debido a esta condición, elegimos una división binaria por »contact_unknownaunque» (aunque estoagecondujo a un coeficiente de Gini más bajo).
Además, suelo limitar lo min_impurity_decreaseque nos impide avanzar más si las ganancias son demasiado pequeñas. Por ganancias, nos referimos a la disminución del coeficiente de Gini.
Entonces, hemos entendido cómo funciona el clasificador de árbol de decisiones y ahora es el momento de usarlo en la práctica.
Si estás interesado en ver cómo funciona el regresor de árbol de decisión con todo detalle, puedes buscarlo en mi artículo anterior .
Árboles de decisión: práctica
Ya hemos creado un modelo de árbol simple con dos capas, pero definitivamente no es suficiente, ya que es demasiado simple extraer toda la información de los datos. Entrenemos otro árbol de decisión limitando el número de muestras en las hojas y disminuyendo la impureza (reducción del coeficiente de Gini).
modelo = sklearn.tree.DecisionTreeClassifier(
min_samples_leaf = 1000 , min_impurity_decrease = 0.001 )
modelo.fit(fin_df[características], fin_df[ 'y' ])
datos_de_punto = sklearn.tree.export_graphviz(
modelo, archivo_de_salida = None , nombres_de_características = features, relleno = True ,
proporción = True , precisión = 2 , impureza = True )
gráfico = graphviz.Source(dot_data)
# guardando el gráfico en un archivo png
png_bytes = graph.pipe( formato = 'png' )
con abierto ( 'decision_tree.png' , 'wb' ) como f:
f.write(png_bytes)

Listo. Tenemos nuestras reglas para dividir a los clientes en grupos (hojas). Ahora, podemos iterar entre los grupos y ver qué grupos de clientes queremos contactar. Aunque nuestro modelo es relativamente pequeño, resulta complicado copiar todas las condiciones de la imagen. Por suerte, podemos analizar la estructura de árbol y obtener todos los grupos del modelo.
El clasificador de árbol de decisión tiene un atributo tree_que nos permitirá acceder a atributos de bajo nivel del árbol, como por ejemplo node_count.
n_nodos = modelo.árbol_.número_de_nodos
print (n_nodos)
# 13
La tree_variable también almacena toda la estructura del árbol como matrices paralelas, donde el ielemento -ésimo de cada matriz almacena la información sobre el nodo i. Para la raíz, iel valor es 0.
Aquí están las matrices que tenemos para representar la estructura del árbol:
children_leftychildren_right— ID de los nodos izquierdo y derecho, respectivamente; si el nodo es una hoja, entonces -1.feature— característica utilizada para dividir el nodoi.threshold— valor umbral utilizado para la división binaria del nodoi.n_node_samples— número de muestras de entrenamiento que llegaron al nodoi.values— acciones de muestras de cada clase.
Guardemos todas estas matrices.
niños_izquierda = modelo.árbol_.niños_izquierda
# [ 1, 2, 3, 4, 5, 6, -1, -1, -1, -1, -1, -1, -1]
niños_derecha = modelo.árbol_.niños_derecha
# [12, 11, 10, 9, 8, 7, -1, -1, -1, -1, -1, -1, -1]
características = modelo.árbol_.característica
# [30, 34, 0, 3, 6, 6, -2, -2, -2, -2, -2, -2, -2]
umbrales = modelo.árbol_.umbral
# [ 0.5, 0.5, 59.5, 0.5, 6.5, 2.5, -2. , -2. , -2. , -2. , -2. , -2. ]
num_nodes = modelo.árbol_.n_muestras_de_nodos
# [45211, 43700, 30692, 29328, 14165, 4165, 2053, 2112, 10000,
# 15163, 1364, 13008, 1511]
values = modelo.árbol_.valor
# [[[0.8830152, 0.1169848]],
# [[0.90135011, 0.09864989]],
# [[0.87671054, 0.12328946]],
# [[0.88550191, 0.11449809]],
# [[0.8530886 , 0,1469114 ]],
# [[0,76686675, 0,23313325]],
# [[0,87043351, 0,12956649]],
# [[0,66619318, 0,33380682]],
# [[0,889 , 0,111 ]],
# [[0,91578184, 0,08421816]],
# [[0,68768328, 0,31231672]],
# [[0,95948647, 0,04051353]],
# [[0,35274653, 0,64725347]]]
Nos resultará más conveniente trabajar con una vista jerárquica de la estructura del árbol, así que iteremos a través de todos los nodos y, para cada nodo, guardemos el ID del nodo padre y si era una rama derecha o izquierda.
jerarquía = {}
para node_id en rango (n_nodos):
si hijos_izquierdo[node_id] != - 1 :
jerarquía[hijos_izquierdo[node_id]] = {
'padre' : node_id,
'condición' : 'izquierda'
}
si hijos_derecho[node_id] != - 1 :
jerarquía[hijos_derecho[node_id]] = {
'padre' : node_id,
'condición' : 'derecha'
}
imprimir (jerarquía)
# {1: {'padre': 0, 'condición': 'izquierda'},
# 12: {'padre': 0, 'condición': 'derecha'},
# 2: {'padre': 1, 'condición': 'izquierda'},
# 11: {'padre': 1, 'condición': 'derecha'},
# 3: {'padre': 2, 'condición': 'izquierda'},
# 10: {'padre': 2, 'condición': 'derecha'},
# 4: {'padre': 3, 'condición': 'izquierda'},
# 9: {'padre': 3, 'condición': 'derecha'},
# 5: {'padre': 4, 'condición': 'izquierda'},
# 8: {'padre': 4, 'condición': 'derecha'},
# 6: {'padre': 5, 'condición': 'izquierda'},
# 7: {'padre': 5, 'condición': 'derecha'}}
El siguiente paso es filtrar los nodos hoja ya que son terminales y los más interesantes para nosotros, ya que definen los segmentos de clientes.
hojas = []
para node_id en el rango (n_nodos):
si (hijos_izquierda[nodo_id] == - 1 ) y (hijos_derecha[nodo_id] == - 1 ):
hojas.append(nodo_id)
print (hojas)
# [6, 7, 8, 9, 10, 11, 12]
hojas_df = pd.DataFrame({ 'nodo_id' : hojas})
El siguiente paso es determinar todas las condiciones aplicadas a cada grupo, ya que definirán nuestros segmentos de clientes. La primera función get_conditionnos proporcionará la tupla de característica, tipo de condición y umbral para un nodo.
def obtener_condición ( id_nodo, condición, características, umbrales, nombres_de_características ):
# print(id_nodo, condición)
característica = nombres_de_características[características[id_nodo]]
umbral = umbrales[id_nodo]
cond = '>' if condición == 'derecha' else '<='
return (característica, cond, umbral)
print (obtener_condición( 0 , 'izquierda' , características, umbrales, nombres_de_características))
# ('poutcome_success', '<=', 0.5)
print (obtener_condición( 0 , 'derecha' , características, umbrales, nombres_de_características))
# ('poutcome_success', ">', 0.5)
La siguiente función nos permitirá ir recursivamente desde el nodo hoja a la raíz y obtener todas las divisiones binarias.
def get_decision_path_rec ( node_id, decision_path, hierarchy ):
if node_id == 0 :
yield decision_path
else :
parent_id = jerarquía[node_id][ 'padre' ]
condition = jerarquía[node_id][ 'condición' ]
for res in get_decision_path_rec(parent_id, decision_path + [(parent_id, condition)], jerarquía):
yield res
decision_path = list (get_decision_path_rec( 12 , [], jerarquía))[ 0 ]
print (decision_path)
# [(0, 'derecha')]
fmt_decision_path = list ( map (
lambda x: get_condition(x[ 0 ], x[ 1 ], features, umbrales, features_names),
decision_path))
print (fmt_decision_path)
# [('poutcome_success', ">', 0.5)]
Guardemos la lógica de ejecutar la recursión y el formato en una función contenedora.
def get_decision_path ( node_id, características, umbrales, jerarquía, nombres_de_características ):
decision_path = list (get_decision_path_rec(node_id, [], jerarquía))[ 0 ]
return list ( map ( lambda x: get_condition(x[ 0 ], x[ 1 ], características, umbrales,
nombres_de_características), decision_path))
Hemos aprendido a obtener las condiciones de división binaria de cada nodo. La única lógica restante es combinar las condiciones.
def get_decision_path_string ( node_id, features, umbrales, jerarquía,
feature_names ):
condiciones_df = pd.DataFrame(get_decision_path(node_id, features, umbrales, jerarquía, feature_names))
condiciones_df.columnas = [ 'característica' , 'condición' , 'umbral' ]
condiciones_izquierda_df = condiciones_df[condiciones_df.condición == '<=' ]
condiciones_derecha_df = condiciones_df[condiciones_df.condición == '>' ]
# deduplicación
condiciones_izquierda_df = condiciones_izquierda_df.groupby([ 'característica' , 'condición' ], como_índice = False ).min ( )
condiciones_derecha_df = condiciones_derecha_df.groupby([ 'característica' , 'condición' ], como_índice = False ). máx ()
# concatenación
fin_conditions_df = pd.concat([left_conditions_df, right_conditions_df])\
.sort_values([ 'característica' , 'condición' ], ascendente = False )
# formato
fin_conditions_df[ 'cond_string' ] = lista ( map (
lambda x, y, z: '(%s %s %.2f)' % (x, y, z),
fin_conditions_df.característica,
fin_conditions_df.condición,
fin_conditions_df.umbral
))
devolver ' y ' .join(fin_conditions_df.cond_string.values)
imprimir (obtener_ruta_de_decisión_string( 12 , características, umbrales, jerarquía,
nombres_de_características))
# (presultado_éxito > 0.50)
Ahora, podemos calcular las condiciones para cada grupo.
leaves_df[ 'condición' ] = leaves_df[ 'id_de_nodo' ]. map (
lambda x: get_decision_path_string(x, características, umbrales, jerarquía,
nombres_de_características)
)
El último paso es agregar su tamaño y conversión a los grupos.
leaves_df[ 'total' ] = leaves_df.id_nodo.map ( lambda x: núm_nodos[x]) leaves_df[ 'conversión' ] = leaves_df[ 'id_nodo' ] .map ( lambda x: valores[x][ 0 ][ 1 ])* 100 leaves_df[ 'usuarios_convertidos' ] = (leaves_df.conversión * leaves_df.total)\ .map ( lambda x : int ( round ( x/ 100 ))) leaves_df[ 'porcentaje_de_convertidos' ] = 100 *leaves_df[ 'usuarios_convertidos' ]/leaves_df[ 'usuarios_convertidos' ]. suma () hojas_df[ 'parte_del_total' ] = 100 *hojas_df[ 'total' ]/hojas_df[ 'total' ]. suma ()
Ahora podemos usar estas reglas para tomar decisiones. Podemos ordenar los grupos por conversión (probabilidad de contacto exitoso) y seleccionar a los clientes con mayor probabilidad.
leaves_df.sort_values( 'conversión' , ascendente = Falso )\
.drop( 'id_nodo' , eje = 1 ).set_index( 'condición' )

Imaginemos que solo tenemos recursos para contactar a alrededor del 10% de nuestra base de usuarios; podemos centrarnos en los tres primeros grupos. Incluso con una capacidad tan limitada, esperamos obtener una conversión de casi el 40%; es un resultado excelente, y lo hemos logrado con solo unas sencillas heurísticas.
En la práctica, también conviene probar el modelo (o la heurística) antes de implementarlo en producción. Yo dividiría el conjunto de datos de entrenamiento en partes de entrenamiento y validación (por tiempo para evitar fugas) y analizaría el rendimiento de la heurística en el conjunto de validación para tener una mejor visión de la calidad real del modelo.
Trabajar con categorías de alta cardinalidad
Otro tema que vale la pena discutir en este contexto es la codificación de categorías, ya que debemos codificar las variables categóricas para sklearnla implementación. Hemos utilizado un enfoque sencillo con codificación one-hot, pero en algunos casos no funciona.
Imaginemos que también tenemos una región en los datos. He generado sintéticamente ciudades inglesas para cada fila. Tenemos 155 regiones únicas, por lo que el número de características ha aumentado a 190.
modelo = sklearn.tree.DecisionTreeClassifier(min_samples_leaf = 100, min_impureza_decrease=0.001)
modelo.fit(fin_df[nombres_de_características], fin_df[ 'y' ])
Entonces, el árbol básico ahora tiene muchas condiciones basadas en regiones y no es conveniente trabajar con ellas.

En tal caso, podría no ser conveniente aumentar el número de características, y es hora de pensar en la codificación. Hay un artículo completo, «Categóricamente: ¡No explotes, codifica!» , que comparte diversas opciones para manejar variables categóricas de alta cardinalidad. Creo que las más viables en nuestro caso serán las dos siguientes:
- Codificador de conteo o frecuencia que muestra un buen rendimiento en las pruebas de referencia. Esta codificación asume que las categorías de tamaño similar tendrían características similares.
- Codificador de Destino, donde podemos codificar la categoría según el valor medio de la variable objetivo. Esto nos permitirá priorizar los segmentos con mayor conversión y despriorizar los segmentos con menor conversión. Idealmente, sería útil usar datos históricos para obtener los promedios de la codificación, pero usaremos el conjunto de datos existente.
Sin embargo, será interesante probar diferentes enfoques, así que dividiremos nuestro conjunto de datos en entrenamiento y prueba, reservando un 10 % para la validación. Para simplificar, he utilizado la codificación one-hot para todas las columnas excepto para la región (ya que tiene la cardinalidad más alta).
de sklearn.model_selection importar train_test_split
fin_df = pd.get_dummies(df, columnas=[ 'trabajo' , 'marital' , 'educación' ,
'resultado' , 'contacto' ], dtype = int , drop_first = False )
train_df, test_df = train_test_split(fin_df,tamaño_prueba= 0.1 , estado_aleatorio= 42 )
imprimir (train_df.shape[ 0 ], test_df.shape[ 0 ])
# (40689, 4522)
Para mayor comodidad, combinemos toda la lógica para analizar el árbol en una sola función.
def obtener_definición_del_modelo ( modelo, nombres_de_características ):
n_nodos = modelo.árbol_.número_de_nodos
hijos_izquierdos = modelo.árbol_.hijos_izquierdos
hijos_derechos = modelo.árbol_.hijos_derechos
características = modelo.árbol_.características
umbrales = modelo.árbol_.umbral
núm_nodos = modelo.árbol_.n_muestras_de_nodos
valores = modelo.árbol_.valor
jerarquía = {}
para id_de_nodo en el rango (n_nodos):
si hijos_izquierdos[id_de_nodo] != - 1 :
jerarquía[hijos_izquierdos[id_de_nodo]] = {
'padre' : id_de_nodo,
'condición' : 'izquierda'
}
si hijos_derecho[id_de_nodo] != - 1 :
jerarquía[hijos_derechos[id_de_nodo]] = {
'padre' : id_de_nodo,
'condición' : 'derecha'
}
hojas = []
para id_de_nodo en el rango (n_nodos):
si (children_left[node_id] == - 1 ) y (children_right[node_id] == - 1 ):
leaves.append(node_id)
leaves_df = pd.DataFrame({ 'node_id' : leaves})
leaves_df[ 'condición' ] = leaves_df[ 'node_id' ]. map (
lambda x: get_decision_path_string(x, features, umbrales, jerarquía, feature_names)
)
leaves_df[ 'total' ] = leaves_df.node_id. map ( lambda x: num_nodes[x])
leaves_df[ 'conversión' ] = leaves_df[ 'node_id' ]. mapa ( lambda x: valores[x][ 0 ][ 1 ])* 100
hojas_df[ 'usuarios_convertidos' ] = (hojas_df.conversión * hojas_df.total). mapa ( lambda x: int ( round (x/ 100 )))
hojas_df[ 'porcentaje_de_convertidos' ] = 100 *hojas_df[ 'usuarios_convertidos' ]/hojas_df[ 'usuarios_convertidos' ].suma ()
hojas_df[ 'parte_del_total' ] = 100 *hojas_df[ 'total' ]/hojas_df[ 'total' ]. suma ()
leaves_df = leaves_df.sort_values( 'conversión' , ascendente = Falso )\
.drop( 'id_nodo' , eje = 1 ).set_index( 'condición' )
leaves_df[ 'participación_acum_del_total' ] = leaves_df[ 'participación_del_total' ].cumsum()
leaves_df[ 'participación_acum_de_convertido' ] = leaves_df[ 'participación_de_convertido' ].cumsum()
return leaves_df
Creemos un marco de datos de codificaciones, calculando frecuencias y conversiones.
codificación_de_región_df = tren_df.groupby( 'región' , como_índice = Falso)\
.agregado({ 'id' : 'recuento' , 'y' : 'media' }). rename (columnas =
{ 'id' : 'recuento_de_región' , 'y' : 'objetivo_de_región' })
Luego, incorpóralos a nuestros conjuntos de entrenamiento y validación. Para el conjunto de validación, también completaremos los NA como promedios.
tren_df = tren_df.merge(región_encoding_df, on = 'región' )
prueba_df = prueba_df.merge(región_encoding_df, on = 'región' , cómo = 'izquierda' )
prueba_df[ 'región_objetivo' ] = prueba_df[ 'región_objetivo' ]\
.fillna(región_encoding_df.región_objetivo.mean())
prueba_df[ 'región_conteo' ] = prueba_df[ 'región_conteo' ]\
.fillna(región_encoding_df.región_conteo.mean())
Ahora podemos ajustar los modelos y obtener sus estructuras.
count_feature_names = train_df.drop(
[ 'y' , 'id' , 'region_target' , 'region' ], axis = 1 ).columns
target_feature_names = train_df.drop(
[ 'y' , 'id' , 'region_count' , 'region' ], axis = 1 ).columns
print ( len (count_feature_names), len (target_feature_names))
# (36, 36)
count_model = sklearn.tree.DecisionTreeClassifier(min_samples_leaf = 500 ,
min_impurity_decrease= 0.001 )
count_model.fit(train_df[count_feature_names], train_df[ 'y' ])
target_model = sklearn.tree.DecisionTreeClassifier(min_samples_leaf = 500 ,
min_impureza_decrease = 0.001 )
target_model.fit(train_df[target_feature_names], train_df[ 'y' ])
count_model_def_df = get_model_definition(count_model, count_feature_names)
target_model_def_df = get_model_definition(target_model, target_feature_names)
Analicemos las estructuras y seleccionemos las categorías principales, que representan hasta el 10-15 % de nuestro público objetivo. También podemos aplicar estas condiciones a nuestros conjuntos de validación para probar nuestro enfoque en la práctica.
Comencemos con Count Encoder.

conteo_df_seleccionado = prueba_df[
(prueba_df.presultado_éxito > 0.50 ) |
((prueba_df.presultado_éxito <= 0.50 ) y (prueba_df.edad > 60.50 )) |
((prueba_df.región_conteo > 3645.50 ) y (prueba_df.región_conteo <= 8151.50 ) y
(prueba_df.presultado_éxito <= 0.50 ) y (prueba_df.contacto_celular > 0.50 ) y (prueba_df.edad <= 60.50 ))
]
imprimir (conteo_df_seleccionado.forma[ 0 ], conteo_df_seleccionado.y. suma ())
# (508, 227)
También podemos ver qué regiones han sido seleccionadas, y sólo Manchester.
codificación_de_región_df[(codificación_de_región_df.recuento_de_región > 3645.50 )
y (codificación_de_región_df.recuento_de_región <= 8151.50 )]

Continuemos con la codificación de destino.

objetivo_seleccionado_df = prueba_df[
((prueba_df.objetivo_región > 0.21 ) y (prueba_df.éxito_resultado > 0.50 )) |
((prueba_df.objetivo_región > 0.21 ) y (prueba_df.éxito_resultado <= 0.50 ) y (prueba_df.mes <= 6.50 ) y (prueba_df.vivienda <= 0.50 ) y (prueba_df.contacto_desconocido <= 0.50 )) |
((prueba_df.objetivo_región > 0,21 ) y (prueba_df.éxito_resultado <= 0,50 ) y (prueba_df.mes > 8,50 ) y (prueba_df.vivienda <= 0,50 )
y (prueba_df.contacto_desconocido <= 0,50 )) |
((prueba_df.objetivo_región <= 0,21 ) y (prueba_df.éxito_resultado > 0,50 )) |
((prueba_df.región_objetivo > 0.21 ) y (prueba_df.resultado_éxito <= 0.50 ) y (prueba_df.mes > 6.50 ) y (prueba_df.mes <= 8.50 )
y (prueba_df.vivienda <= 0.50 ) y (prueba_df.contacto_desconocido <= 0.50 ))
]
imprimir (objetivo_df_seleccionado.forma[ 0 ], objetivo_df_seleccionado.y. suma ())
# (502, 248)
Observamos un número ligeramente menor de usuarios seleccionados para la comunicación, pero un número significativamente mayor de conversiones: 248 frente a 227 (+9,3%).
Analicemos también las categorías seleccionadas. Vemos que el modelo incluyó todas las ciudades con alta tasa de conversión (Mánchester, Liverpool, Bristol, Leicester y New Castle), pero también hay muchas regiones pequeñas con altas tasas de conversión debido únicamente al azar.
codificación_de_región_df[codificación_de_región_df.objetivo_de_región > 0.21 ]\
.sort_values( 'recuento_de_región' , ascendente = Falso)
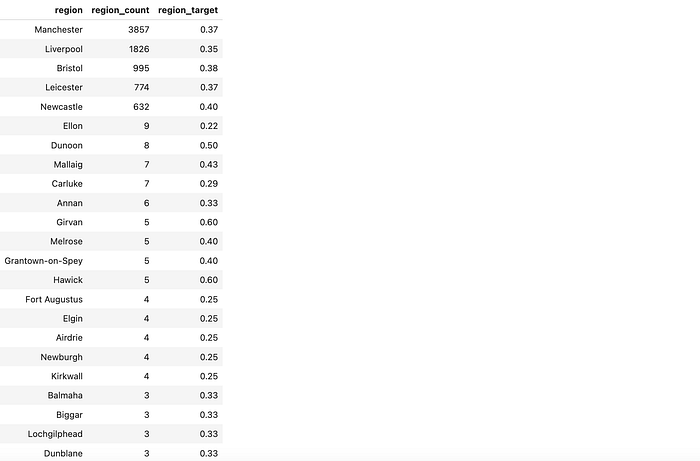
En nuestro caso, no tiene un gran impacto, ya que la proporción de ciudades tan pequeñas es baja. Sin embargo, si tiene muchas más categorías pequeñas, podría observar inconvenientes significativos de sobreajuste. La codificación de destino puede ser complicada en este punto, por lo que conviene vigilar el resultado de su modelo.
Afortunadamente, existe un enfoque que puede ayudarte a solucionar este problema. Siguiendo el artículo «Codificación de variables categóricas: Un análisis profundo de la codificación de destino» , podemos añadir suavizado. La idea es combinar la tasa de conversión del grupo con el promedio general: cuanto mayor sea el grupo, mayor será la ponderación de sus datos, mientras que los segmentos más pequeños se inclinarán más hacia el promedio global.
Primero, seleccioné los parámetros que tienen sentido para nuestra distribución, considerando varias opciones. Opté por usar el promedio global para los grupos de menos de 100 personas. Esta parte es un poco subjetiva, así que use el sentido común y sus conocimientos del sector empresarial.
importar numpy como np
importar matplotlib.pyplot como plt
global_mean = train_df.y.mean()
k = 100
f = 10
smooth_df = pd.DataFrame({ 'recuento_región' :np.arange( 1 , 100001 , 1 ) })
smooth_df[ 'suavizado' ] = ( 1 / ( 1 + np.exp(-(smooth_df.región_count - k) / f)))
ax = plt.scatter(smooth_df.región_count, smooth_df.suavizado)
plt.xscale( 'log' )
plt.ylim([- .1 , 1.1 ])
plt.title( 'Suavizado' )

Luego, podemos calcular, en base a los parámetros seleccionados, los coeficientes de suavizado y los promedios combinados.
codificación_región_df[ 'suavizado' ] = ( 1 / ( 1 + np.exp(-(codificación_región_df.región_cuenta - k) / f)))
codificación_región_df[ 'objetivo_región' ] = codificación_región_df.suavizado * codificación_región_df.objetivo_región_sin procesar \
+ ( 1 - codificación_región_df.suavizado) * media_global
Luego, podemos ajustar otro modelo con codificación de categoría objetivo suavizada.
tren_df = tren_df.merge(codificación_región_df [['región', 'región_objetivo']] , activado = 'región' )
prueba_df = prueba_df.merge(codificación_región_df [['región', 'región_objetivo']] , activado = 'región' , cómo = 'izquierda' )
prueba_df[ 'región_objetivo' ] = prueba_df[ 'región_objetivo' ]\
.fillna(codificación_región_df.región_objetivo.mean())
nombres_de_características_objetivo_v2 = tren_df.drop([ 'y' , 'id' , 'región' ], eje = 1 ).columnas
modelo_v2_objetivo = sklearn.tree.DecisionTreeClassifier(min_samples_leaf = 500 ,
min_impureza_decrease = 0.001 )
target_v2_model.fit(train_df[nombres_de_características_de_objetivo_v2], train_df[ 'y' ])
target_v2_model_def_df = get_model_definition(objetivo_v2_model, nombres_de_características_de_objetivo_v2)

objetivo_v2_df_seleccionado = prueba_df[
((prueba_df.objetivo_región > 0.12 ) y (prueba_df.éxito_resultado > 0.50 )) |
((prueba_df.objetivo_región > 0.12 ) y (prueba_df.éxito_resultado <= 0.50 ) y (prueba_df.mes <= 6.50 ) y (prueba_df.vivienda <= 0.50 ) y (prueba_df.contacto_desconocido <= 0.50 )) |
((prueba_df.objetivo_región > 0,12 ) y (prueba_df.éxito_resultado <= 0,50 ) y (prueba_df.mes > 8,50 ) y (prueba_df.vivienda <= 0,50 )
y (prueba_df.contacto_desconocido <= 0,50 )) |
((prueba_df.objetivo_región <= 0,12 ) y (prueba_df.éxito_resultado > 0,50 )) |
((prueba_df.región_objetivo > 0.12 ) y (prueba_df.resultado_éxito <= 0.50 ) y (prueba_df.mes > 6.50 ) y (prueba_df.mes <= 8.50 )
y (prueba_df.vivienda <= 0.50 ) y (prueba_df.contacto_desconocido <= 0.50 ) )
]
objetivo_v2_df_seleccionado.forma[ 0 ], objetivo_v2_df_seleccionado.y. suma ()
# (500, 247)
Podemos ver que hemos eliminado las ciudades pequeñas y evitado el sobreajuste en nuestro modelo manteniendo aproximadamente el mismo rendimiento, capturando 247 conversiones.
codificación_de_región_df [codificación_de_región_df.objetivo_de_región > 0.1173]

También puedes usar TargetEncoder de sklearn, que suaviza y mezcla las medias de categoría y globales según el tamaño del segmento. Sin embargo, también añade ruido aleatorio, lo cual no es ideal para nuestro caso de heurística.
Puedes encontrar el código completo en GitHub .
Resumen
En este artículo, exploramos cómo extraer «reglas» simples de los datos y usarlas para fundamentar decisiones empresariales. Generamos heurísticas mediante un clasificador de árboles de decisión y abordamos el importante tema de la codificación categórica, ya que los algoritmos de árboles de decisión requieren la conversión de variables categóricas.
Vimos que este enfoque basado en reglas puede ser sorprendentemente eficaz, ayudándole a tomar decisiones de negocio rápidamente. Sin embargo, cabe destacar que este enfoque simplista tiene sus inconvenientes:
- Estamos negociando la potencia y precisión del modelo por su simplicidad e interpretabilidad, así que si está optimizando para lograr precisión, elija otro enfoque.
- Aunque utilizamos un conjunto de heurísticas estáticas, sus datos aún pueden cambiar y pueden quedar desactualizados, por lo que deberá volver a verificar su modelo de vez en cuando.
Muchas gracias por leer este artículo. Espero que te haya resultado útil. Si tienes alguna pregunta o comentario, déjalo en la sección de comentarios.
Referencia
Todas las imágenes son producidas por el autor a menos que se indique lo contrario.
Conjunto de datos: Moro, S., Rita, P. y Cortez, P. (2014). Marketing bancario [Conjunto de datos]. Repositorio de aprendizaje automático de la UCI. https://doi.org/10.24432/C5K306




